题目内容
(1)证明函数f(x)=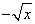 在定义域上是减函数;
在定义域上是减函数;
(2)证明函数f(x)=x3+x在R上是增函数.
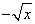 在定义域上是减函数;
在定义域上是减函数;(2)证明函数f(x)=x3+x在R上是增函数.
证明:(1)f(x)=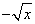 的定义域为[0,+∞),
的定义域为[0,+∞),
设0≤x1<x2,则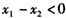 ,
,
且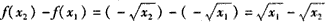
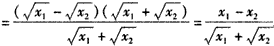 ,
,
∵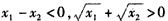 ,
,
∴f(x2)-f(x1)<0,即f(x2)<f(x1),
∴f(x)=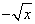 在它的定义域[0,+∞)上是减函数.
在它的定义域[0,+∞)上是减函数.
(2)设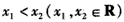 ,则
,则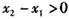 ,
,
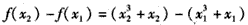
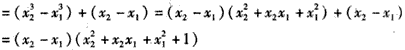
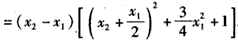 ,
,
∵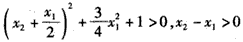 ,
,
∴f(x2)-f(x1)>0,即f(x2)>f(x1),
∴f(x)=x3+x在R上是增函数。
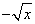 的定义域为[0,+∞),
的定义域为[0,+∞),设0≤x1<x2,则
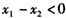 ,
,且
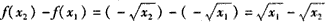
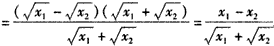 ,
,∵
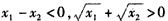 ,
,∴f(x2)-f(x1)<0,即f(x2)<f(x1),
∴f(x)=
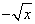 在它的定义域[0,+∞)上是减函数.
在它的定义域[0,+∞)上是减函数.(2)设
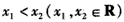 ,则
,则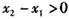 ,
,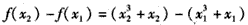
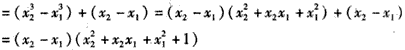
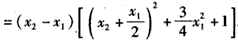 ,
,∵
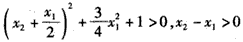 ,
,∴f(x2)-f(x1)>0,即f(x2)>f(x1),
∴f(x)=x3+x在R上是增函数。

练习册系列答案
相关题目
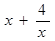 在
在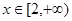 上是增函数;
上是增函数;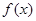 在
在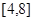 上的值域。
上的值域。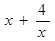 在
在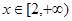 上是增函数;
上是增函数;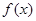 在
在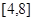 上的值域。
上的值域。