题目内容

是否存在4个平面向量，两两不共线，其中任何两个向量之和均与其余两个向量之和垂直？

答案：
解析：

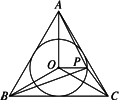
　　如图所示，在正△ABC中，O为其内心，P为圆周上一点，满足、、两两不共线，有(＋)·(＋)

　　＝(＋＋＋)·(＋＋)

　　＝(2＋＋)·(2＋)

　　＝(2－)·(2＋)

　　＝42－2

　　＝0．

　　∴有(＋)与(＋)垂直．

　　同理可证其他情况．

　　从而、、、满足题意．故存在这样的4个平面向量．


提示：

本题是一个探索性问题，解决本题的关键在于构造一个正三角形及其内切圆，得到四个向量，这也是本题的难点．然后利用向量之间的关系，运用数量积的运算律论证＋与＋垂直．


练习册系列答案
相关题目
在中学阶段，对许多特定集合（如实数集、复数集以及平面向量集等）的学习常常是以定义运算（如四则运算）和研究运算律为主要内容．现设集合A由全体二元有序实数组组成，在A上定义一个运算，记为⊙，对于A中的任意两个元素α=（a，b），β=（c，d），规定：α⊙β=(
.
a-c
bd
.
，
.
da
cb
.
)．
（1）计算：（2，3）⊙（-1，4）；
（2）请用数学符号语言表述运算⊙满足交换律和结合律，并任选其一证明；
（3）A中是否存在唯一确定的元素I满足：对于任意α∈A，都有α⊙I=I⊙α=α成立，若存在，请求出元素I；若不存在，请说明理由；
（4）试延续对集合A的研究，请在A上拓展性地提出一个真命题，并说明命题为真的理由．
在平面直角坐标系中，已知三个点列{An}，{Bn}，{Cn}，其中An（n，an），Bn（n，bn），Cn（n-1，0），满足向量
AnAn+1
与向量
BnCn
平行，并且点列{Bn}在斜率为6的同一直线上，n=1，2，3，…．
（1）证明：数列{bn}是等差数列；
（2）试用a1，b1与n表示an（n≥2）；
（3）设a1=a，b1=-a，是否存在这样的实数a，使得在a6与a7两项中至少有一项是数列{an}的最小项？若存在，请求出实数a的取值范围；若不存在，请说明理由；
（4）若a1=b1=3，对于区间[0，1]上的任意λ，总存在不小于2的自然数k，当n≥k时，an≥（1-λ）（9n-6）恒成立，求k的最小值．

是否存在4个平面向量，两两不共线，其中任何两个向量之和均与其余两个向量之和垂直？
在中学阶段，对许多特定集合（如实数集、复数集以及平面向量集等）的学习常常是以定义运算（如四则运算）和研究运算律为主要内容．现设集合A由全体二元有序实数组组成，在A上定义一个运算，记为⊙，对于A中的任意两个元素α=（a，b），β=（c，d），规定：α⊙β=．
（1）计算：（2，3）⊙（-1，4）；
（2）请用数学符号语言表述运算⊙满足交换律和结合律，并任选其一证明；
（3）A中是否存在唯一确定的元素I满足：对于任意α∈A，都有α⊙I=I⊙α=α成立，若存在，请求出元素I；若不存在，请说明理由；
（4）试延续对集合A的研究，请在A上拓展性地提出一个真命题，并说明命题为真的理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网