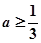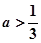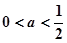题目内容
.要将两种大小不同的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格的小钢板块数如下表:
今需A、B、C三种规格的成品各15、18、27块,所需两种规格的钢板的张数分别为m、n(m、n为整数),则m+n的最小值为 ( )
A.10 B.11 C.12 D.13
| | A规格 | B规格 | C规格 |
| 第一种钢板 | 2 | 1 | 1 |
| 第二种钢板 | 1 | 2 | 3 |
今需A、B、C三种规格的成品各15、18、27块,所需两种规格的钢板的张数分别为m、n(m、n为整数),则m+n的最小值为 ( )
A.10 B.11 C.12 D.13
C
解:设需截第一种钢板x张,第二种钢板y张,所用钢板数为z,
则有 2x+y≥15, x+2y≥18, x+3y≥27 ,x∈N y∈N ,作出可行域(如图)
目标函数为z=x+y
作出一组平行直线x+y=t(t为参数).
由 2x+y="15" x+3y=27 得T(18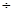 5 ,39
5 ,39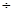 5 ),由于点T不是可行域内的整数点,而在可行域内的整数点中,点(4,8)和点(3,9)使z最小,且最小值为:4+8=3+9=12.
5 ),由于点T不是可行域内的整数点,而在可行域内的整数点中,点(4,8)和点(3,9)使z最小,且最小值为:4+8=3+9=12.
故答案为:C
则有 2x+y≥15, x+2y≥18, x+3y≥27 ,x∈N y∈N ,作出可行域(如图)
目标函数为z=x+y
作出一组平行直线x+y=t(t为参数).
由 2x+y="15" x+3y=27 得T(18
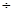 5 ,39
5 ,39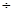 5 ),由于点T不是可行域内的整数点,而在可行域内的整数点中,点(4,8)和点(3,9)使z最小,且最小值为:4+8=3+9=12.
5 ),由于点T不是可行域内的整数点,而在可行域内的整数点中,点(4,8)和点(3,9)使z最小,且最小值为:4+8=3+9=12.故答案为:C

练习册系列答案
相关题目
 满足约束条件
满足约束条件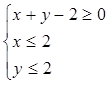 ,
,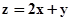 的最大值和最小值.
的最大值和最小值. 满足
满足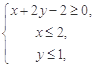 ,则
,则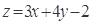 的最大值为( )
的最大值为( )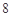

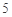
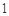
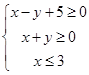 ,则
,则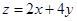 的最大值为
的最大值为 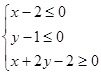 表示的平面区域内运动,则
表示的平面区域内运动,则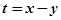 的取值范围是( )
的取值范围是( )
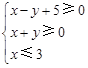 ,
,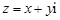 (
(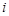 为虚数单位),则
为虚数单位),则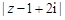 的最小值是 .
的最小值是 .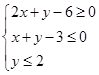 表示的平面区域的面积为( )
表示的平面区域的面积为( )
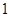
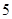
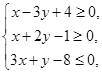 若目标函数
若目标函数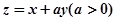 恰好在点(2,2)处取得最大值,则
恰好在点(2,2)处取得最大值,则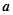 的取值范围为( )
的取值范围为( )