题目内容

△ABC满足
AB
•
AC
=2
3
，∠BAC=30°，设M是△ABC内的一点（不在边界上），定义f（M）=（x，y，z），其中x，y，z分别表示△MBC，△MCA，△MAB的面积，若f（M）=（x，y，
1
2
），则xy的最大值为（　　）
分析：由向量的数量积公式，求出|
AB
|•|
AC
|=4，由题意得，x+y=
1
2
．然后通过基本不等式求出xy的最大值，即可得答案．
解答：解：∵
AB
•
AC
=2
3
，∠BAC=30°，
所以由向量的数量积公式得|
AB
|•|
AC
|•cos∠BAC=2
3
，
∴|
AB
|•|
AC
|=4，
∵S△ABC=
1
2
|
AB
|•|
AC
|•sin∠BAC=1．
由题意得，
x+y=1-
1
2
=
1
2
．
所以xy=
xy
4×
1
4
=
xy
4×(x+y)2
=
1
4(
x
y
+
y
x
+2)
≤
1
16
，
当且仅当x=y=
1
4
时，xy取得最大值
1
16
．
故选C．
点评：本题考查基本不等式的应用和向量的数量积的应用，解题时要认真审题，注意公式的灵活运用．
练习册系列答案
相关题目
△ABC满足
AB
•
AC
=2
3
，∠BAC=30°，设M是△ABC内的一点（不在边界上），定义f（M）=（x，y，z），其中x，y，z分别表示△MBC，△MCA，△MAB的面积，若f（M）=（x，y，
1
2
），则
1
x
+
4
y
的最小值为（　　）
A、9B、8C、18D、16
对于△ABC内的任何一点M，为了确定M的具体位置f（M），采用如下记法：f（M）=（x，y，z），x，y，z分别表示△MBC，△MCA，△MAB的面积，现有△ABC满足
AB
•
AC
=2
3
且∠A=30°，设M是△ABC内的一点（不在边界上），当f(M)=(x，y，
1
2
)，那么
1
x
+
4
y
的最小值为
18
18
．
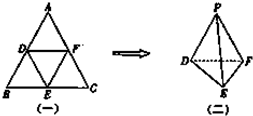如图（一）等腰三角形ABC满足AB=AC=10，BC=12，D、E、F为AB、BC、AC的中点，现将△ADF、△BDE、△CEF分别沿DF、DE、EF折起使得A、B、C重合为一点P，形成一个三棱锥P-DEF如图（二），则三棱锥P-DEF的体积为（　　）
平面直角坐标系中，△ABC满足
AB
=(-
3
sinθ，sinθ)，
AC
=(cosθ，sinθ)，
（Ⅰ）若BC边长等于1，求θ的值（只需写出（0，2π）内的θ值）；
（Ⅱ）若θ恰好等于内角A，求此时内角A的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网