题目内容
已知M>-3,设命题p:曲线 +
+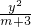 =1表示焦点在y轴上的椭圆,命题q:当0<x<2时,函数f(x)=x+
=1表示焦点在y轴上的椭圆,命题q:当0<x<2时,函数f(x)=x+ >m恒成立.
>m恒成立.
(Ⅰ) 若“p∧q”为真命题,求m的取值范围;
(Ⅱ) 若“p∨q”为真命题,“p∧q”为假命题,求m的取值范围.
解:∵m>-3,命题p:曲线 +
+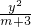 =1表示焦点在y轴上的椭圆,∴m+3>2,解得m>-1.
=1表示焦点在y轴上的椭圆,∴m+3>2,解得m>-1.
∵m>-3,命题q:当0<x<2时,函数f(x)=x+ >m恒成立.∴m>-3,m<[f(x)]min.
>m恒成立.∴m>-3,m<[f(x)]min.
∵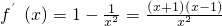 ,∴x∈(0,1)时,f′(x)<0;x∈(1,2)时,f′(x)>0.故在x=1处取得最小值,且f(1)=2,
,∴x∈(0,1)时,f′(x)<0;x∈(1,2)时,f′(x)>0.故在x=1处取得最小值,且f(1)=2,
∴-3<m<2.
(Ⅰ)∵“p∧q”为真命题,∴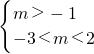 ,解得-1<m<2,即为m的取值范围.
,解得-1<m<2,即为m的取值范围.
(Ⅱ)∵“p∨q”为真命题,“p∧q”为假命题,∴命题p与q必有一个为真,一个为假.
①若p真q假,则 ,解得m≥2,即为m的取值范围.
,解得m≥2,即为m的取值范围.
②若p假q真,则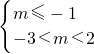 ,解得-3<m≤-1,即为m的取值范围.
,解得-3<m≤-1,即为m的取值范围.
分析:先化简命题p、q,(Ⅰ)根据“p∧q”为真命题,则命题p、q皆为真命题,即可求出;
(Ⅱ)由“p∨q”为真命题,“p∧q”为假命题,∴命题p与q必有一个为真,一个为假,据此即可求出.
点评:熟练掌握椭圆的性质及不等式的恒成立问题的解法及“∧”“∨”命题的真假判断是解题的关键.
 +
+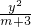 =1表示焦点在y轴上的椭圆,∴m+3>2,解得m>-1.
=1表示焦点在y轴上的椭圆,∴m+3>2,解得m>-1.∵m>-3,命题q:当0<x<2时,函数f(x)=x+
 >m恒成立.∴m>-3,m<[f(x)]min.
>m恒成立.∴m>-3,m<[f(x)]min.∵
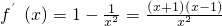 ,∴x∈(0,1)时,f′(x)<0;x∈(1,2)时,f′(x)>0.故在x=1处取得最小值,且f(1)=2,
,∴x∈(0,1)时,f′(x)<0;x∈(1,2)时,f′(x)>0.故在x=1处取得最小值,且f(1)=2,∴-3<m<2.
(Ⅰ)∵“p∧q”为真命题,∴
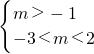 ,解得-1<m<2,即为m的取值范围.
,解得-1<m<2,即为m的取值范围.(Ⅱ)∵“p∨q”为真命题,“p∧q”为假命题,∴命题p与q必有一个为真,一个为假.
①若p真q假,则
 ,解得m≥2,即为m的取值范围.
,解得m≥2,即为m的取值范围.②若p假q真,则
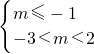 ,解得-3<m≤-1,即为m的取值范围.
,解得-3<m≤-1,即为m的取值范围.分析:先化简命题p、q,(Ⅰ)根据“p∧q”为真命题,则命题p、q皆为真命题,即可求出;
(Ⅱ)由“p∨q”为真命题,“p∧q”为假命题,∴命题p与q必有一个为真,一个为假,据此即可求出.
点评:熟练掌握椭圆的性质及不等式的恒成立问题的解法及“∧”“∨”命题的真假判断是解题的关键.

练习册系列答案
相关题目
 +
+ =1表示焦点在y轴上的椭圆,命题q:当0<x<2时,函数f(x)=x+
=1表示焦点在y轴上的椭圆,命题q:当0<x<2时,函数f(x)=x+ >m恒成立.
>m恒成立.