题目内容
【题目】正三棱柱ABC﹣A1B1C1底边长为2,E,F分别为BB1 , AB的中点. (I)已知M为线段B1A1上的点,且B1A1=4B1M,求证:EM∥面A1FC;
(II)若二面角E﹣A1C﹣F所成角的余弦值为 ![]() ,求AA1的值.
,求AA1的值.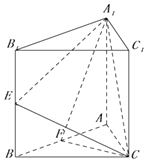
【答案】证明:(I)取B1A1中点为N,连结BN, 则BN∥A1F,又B1A1=4B1M,
则EM∥BN,所以EM∥A1F,
因为EM面A1FC,A1F面A1FC,
故EM∥面A1FC.
解:(II)如图,以F为坐标原点建立空间直角坐标系,
设AA1=a.
则 ![]() ,
,![]() ,
,
设平面A1CF法向量为 ![]() ,
,
设平面A1EF法向量为 ![]() .
.
则  ,取z=1,得
,取z=1,得 ![]() ,
, ,取x=1,得
,取x=1,得 ![]() ;
;
设二面角E﹣A1C﹣F的平面角为θ,
∵二面角E﹣A1C﹣F所成角的余弦值为 ![]() ,
,
∴ ![]() ,
,
设a2=t,则9t2+10t﹣111=0,得t=3,
即a2=3,∴ ![]() .
.
【解析】(I)取B1A1中点为N,连结BN,推导出BN∥A1F,从而EM∥BN,进而EM∥A1F,由此能证明EM∥面A1FC.(II)以F为坐标原点建立空间直角坐标系,设AA1=a,利用向量法能求出结果.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.

练习册系列答案
相关题目
【题目】随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
时间代号t | 1 | 2 | 3 | 4 | 5 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
(1)求y关于t的回归方程![]()
(2)用所求回归方程预测该地区2015年(![]() )的人民币储蓄存款.
)的人民币储蓄存款.
附:回归方程![]() 中
中