题目内容
已知函数f(x)的定义域为(-2,2)导函数为f´(x)=2+cosx且f(0)=0,则满足f(1+x)+f(x-x2)>0的实数x的
取值范围为
(A)(-1,1) (B) (C)
(C) (D)
(D)
【答案】
C
【解析】解:因为由题意,可知函数f(x)的定义域为(-2,2)导函数为f´(x)=2+cosx且f(0)=0,,所以函数在定义域内单调递增,那么并且原函数为f(x)=2x+sinx+c,因为f(0)=0,,所以c=0,则f(x)=2x+sinx是奇函数,所以原不等式f(1+x)+f(x-x2)>0等价于f(1+x)>-f(x-x2)= f(-x+x2)
同时要满足
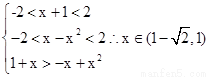

练习册系列答案
相关题目