题目内容
已知f(x)=2sinx(cosx-sinx),其中x∈R
(1)求函数f(x)的最小正周期,并从下列的变换中选择一组合适变换的序号,经过这组变换的排序,可以把函数y=sin2x的图象变成y=f(x)的图象;(要求变换的先后顺序)
①纵坐标不变,横坐标变为原来的
倍,
②纵坐标不变,横坐标变为原来的2倍,
③横坐标不变,纵坐标变为原来的
倍,
④横坐标不变,纵坐标变为原来的
倍,
⑤向上平移一个单位,⑥向下平移一个单位,
⑦向左平移
个单位,⑧向右平移
个单位,
⑨向左平移
个单位,⑩向右平移
个单位,
(2)在△ABC中角A,B,C对应边分别为a,b,c,f(A)=0,b=4,S△ABC=6,求a的长.
(1)求函数f(x)的最小正周期,并从下列的变换中选择一组合适变换的序号,经过这组变换的排序,可以把函数y=sin2x的图象变成y=f(x)的图象;(要求变换的先后顺序)
①纵坐标不变,横坐标变为原来的
| 1 |
| 2 |
②纵坐标不变,横坐标变为原来的2倍,
③横坐标不变,纵坐标变为原来的
| 2 |
④横坐标不变,纵坐标变为原来的
| ||
| 2 |
⑤向上平移一个单位,⑥向下平移一个单位,
⑦向左平移
| π |
| 4 |
| π |
| 4 |
⑨向左平移
| π |
| 8 |
| π |
| 8 |
(2)在△ABC中角A,B,C对应边分别为a,b,c,f(A)=0,b=4,S△ABC=6,求a的长.
分析:(1)根据二倍角的三角函数公式和辅助角公式,化简得f(x)=
sin(2x+
)-1,由三角函数的周期公式可算出最小正周期为T=π,结合三角函数图象变换的方法,可得y=sin2x的图象按照⑨③⑥或③⑨⑥的顺序变换,可得y=f(x)的图象;
(2)由(1)的解析式,结合三角形内角的范围解出A=
,代入三角形面积公式算出c=3
,最后利用余弦定理即可算出边a的长.
| 2 |
| π |
| 4 |
(2)由(1)的解析式,结合三角形内角的范围解出A=
| π |
| 4 |
| 2 |
解答:解:(1)f(x)=2sinx(cosx-sinx)=sin2x-2sin2x=sin2x+cos2x-1=
sin(2x+
)-1…(3分)
∴f(x)的最小正周期为T=
=π …(5分)
把y=sin2x的图象向左平移
,然后横坐标不变、纵坐标变为原来
倍,
再向下平移1个单位得到函数y=f(x)的图象.按照⑨③⑥或③⑨⑥的顺序变换即可…(8分)
(2)∵f(A)=0,即sin(2A+
)=
,且2A+
∈(
,
)
∴2A+
=
,解之得A=
…(10分)
S△ABC=
bcsinA=
×4×csin
=6,解之得c=3
…(10分)
根据余弦定理,得a2=b2+c2-2bccosA=16+18-2×4×3
cos
=10
∴a=
(舍负)…(14分).
| 2 |
| π |
| 4 |
∴f(x)的最小正周期为T=
| 2π |
| 2 |
把y=sin2x的图象向左平移
| π |
| 8 |
| 2 |
再向下平移1个单位得到函数y=f(x)的图象.按照⑨③⑥或③⑨⑥的顺序变换即可…(8分)
(2)∵f(A)=0,即sin(2A+
| π |
| 4 |
| ||
| 2 |
| π |
| 4 |
| π |
| 4 |
| 9π |
| 4 |
∴2A+
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 4 |
| 2 |
根据余弦定理,得a2=b2+c2-2bccosA=16+18-2×4×3
| 2 |
| π |
| 4 |
∴a=
| 10 |
点评:本题将三角函数式化简,求函数的周期和图象的变换,并依此解三角形ABC.着重考查了三角恒等变换、三角函数的图象与性质和正余弦定理等知识,属于中档题.

练习册系列答案
相关题目
 倍,
倍,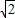 倍,
倍,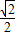 倍,
倍, 个单位,⑧向右平移
个单位,⑧向右平移 个单位,
个单位, 个单位,⑩向右平移
个单位,⑩向右平移 个单位,
个单位,