Question

一个几何体的三视图如图所示,且其侧视图是一个等边三角形,则这个几何的体积为（ ）

A．	B．
C．	D．

Answer 1

D

解析试题分析：观察三视图知，该几何体是半个圆锥与一个四棱锥的组合体。因为，其侧视图是一个边长为2的等边三角形,所有，几何体高为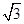。圆锥底半径为1，四棱锥底面边长为2，故其体积为，，选D。
考点：三视图，体积计算。
点评：简单题，三视图问题，关键是理解三视图的画法规则，应用“长对正，高平齐，宽相等”，确定数据。认识几何体的几何特征，是解题的关键之一。