题目内容
若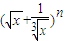
的展开式中的各项系数之和大于8且小于32，则展开式中系数最大的项为 ．
【答案】分析：令x=1，可求出展开式中的各项系数之和，由已知求出n=4，注意到展开式中各项系数等于各项的二项式系数，故中间项即第3项系数最大．
解答：解：由已知，令x=1，展开式中的各项系数之和为2n∴8＜2n＜32∴n=4．
展开式中各项系数等于各项的二项式系数，系数最大的项为第3项，为
故答案为：6
．
点评：本题考查二项式定理的应用，考查赋值思想、求指定的项．属于基础题．
解答：解：由已知，令x=1，展开式中的各项系数之和为2n∴8＜2n＜32∴n=4．
展开式中各项系数等于各项的二项式系数，系数最大的项为第3项，为
故答案为：6
．点评：本题考查二项式定理的应用，考查赋值思想、求指定的项．属于基础题．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
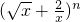展开式中的常数项等于________．
展开式中的常数项等于 ．
的展开式中，各项系数的和与各项二项式系数的和之比为512，那么
展开式中的常数项等于 。
的展开式中，各项系数的和与各项二项式系数的和之比为512，那么
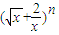展开式中的常数项等于 。