题目内容
已知直线AB、CD是异面直线，AC⊥CD，BD⊥CD，且AB=2，CD=1，则异面直线AB与CD所成角的大小为（ ）
分析：作过CD与AC垂直的平面α，设B在平面α上的投影为B′，由已知中BD⊥CD，AB在平面α上的射影为CB′，根据三垂线定理我们易得∠CDB′=90°，根据AB=2，CD=1，解△CDB′，即可求出异面直线AB与CD所成角的大小．
解答：解：作过CD与AC垂直的平面α，设B在平面α上的投影为B′，
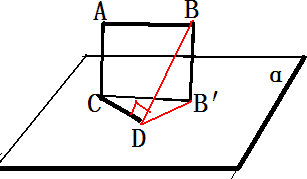
∵BB′⊥α，由三垂线定理可得：
∠CDB′=90°，AB∥CB′，且AB=AB′
∴CB′=2．CD=1
∴AB与CD所成角=∠DCB′=60°
故选C．
∵BB′⊥α，由三垂线定理可得：
∠CDB′=90°，AB∥CB′，且AB=AB′
∴CB′=2．CD=1
∴AB与CD所成角=∠DCB′=60°
故选C．
点评：本题考查的知识点是异面直线及其所成的角，其中利用三垂线定理，将异面直线的夹角转化为解三角形问题是解答本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
16、如图：已知平面α∥平面β，点A、B在平面α内，点C、D在β内，直线AB与CD是异面直线，点E、F、G、H分别是线段AC、BC、BD、AD的中点，求证：
//平面
,点A、B在平面