题目内容
下列命题中,真命题是
- A.?m∈R,使函数f(x)=x2+mx(x∈R)是偶函数
- B.?m∈R,使函数f(x)=x2+mx(x∈R)是奇函数
- C.?m∈R,使函数f(x)=x2+mx(x∈R)都是偶函数
- D.?m∈R,使函数f(x)=x2+mx(x∈R)都是奇函数
A
分析:本题主要考查函数奇偶性的基本概念即在定义域内对于任意的x都有f(-x)=-f(x),则f(x)是奇函数,在定义域内对于任意的x都有f(-x)=f(x),则f(x)是偶函数,还考查了存在量词、全称量词的含义与应用,属于容易题.
解答:A、当m=0时,函数f(x)=x2是偶函数,故A正确;
B、f(-x)=x2-mx,-f(x)=-x2-mx,不存在m使函数在定义域内对任意的x都有f(-x)=-f(x),故B错误;
C、仅当m=0时f(x)是偶函数,m取其它值均不满足题意,故C错误;
D、一个m也没有更谈不上对任意的m的值,故D错误.
故选A.
点评:本题主要是函数奇偶性的应用,判断函数奇偶性有两步①定义域是否关于原点对称②若定义域关于原点对称则再看f(-x)与f(x)的关系,有时奇偶性的判断也可以根据函数的图象.
分析:本题主要考查函数奇偶性的基本概念即在定义域内对于任意的x都有f(-x)=-f(x),则f(x)是奇函数,在定义域内对于任意的x都有f(-x)=f(x),则f(x)是偶函数,还考查了存在量词、全称量词的含义与应用,属于容易题.
解答:A、当m=0时,函数f(x)=x2是偶函数,故A正确;
B、f(-x)=x2-mx,-f(x)=-x2-mx,不存在m使函数在定义域内对任意的x都有f(-x)=-f(x),故B错误;
C、仅当m=0时f(x)是偶函数,m取其它值均不满足题意,故C错误;
D、一个m也没有更谈不上对任意的m的值,故D错误.
故选A.
点评:本题主要是函数奇偶性的应用,判断函数奇偶性有两步①定义域是否关于原点对称②若定义域关于原点对称则再看f(-x)与f(x)的关系,有时奇偶性的判断也可以根据函数的图象.

练习册系列答案
相关题目
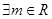 ,使函数
,使函数 是偶函数
是偶函数 ,使函数
,使函数 ≤0
≤0 =-1
=-1