题目内容
已知双曲线的两条渐近线经过坐标原点,且与以A(
,0)为圆心,1为半径的圆相切,双曲线的一个顶点A'与点A关于直线y=x对称.
(1)求双曲线的方程;
(2)是否存在过A点的一条直线交双曲线于M、N两点,且线段MN被直线x=-1平分.如果存在,求出直线的方程;如果不存在,说明理由.
| 2 |
(1)求双曲线的方程;
(2)是否存在过A点的一条直线交双曲线于M、N两点,且线段MN被直线x=-1平分.如果存在,求出直线的方程;如果不存在,说明理由.
分析:(1)先确定双曲线顶点的坐标,再利用双曲线的渐近线经过坐标原点,且与以A(
,0)为圆心,1为半径的圆相切,求得渐近线方程,从而求出双曲线的方程;
(2)先假设存在,与双曲线方程联立,利用线段MN被直线x=-1平分,求参数的值,再进行验证即可.
| 2 |
(2)先假设存在,与双曲线方程联立,利用线段MN被直线x=-1平分,求参数的值,再进行验证即可.
解答:解:(1)由题意得,∵双曲线的一个顶点A'与点A关于直线y=x对称
∴顶点A'(0,
)
设双曲线的一条渐近线方程为y=kx
∵双曲线的渐近线经过坐标原点,且与以A(
,0)为圆心,1为半径的圆相切
∴k=1
∴双曲线的方程为
-
=1
(2)设过A点的一条直线方程为y=m(x-
),
代入双曲线方程并化简得(m2-1)x2-2
m2x+2m2-2=0
由题意,
=-1,即m=±
经验证,满足题意
∴直线方程为y=±
(x-
)
∴顶点A'(0,
| 2 |
设双曲线的一条渐近线方程为y=kx
∵双曲线的渐近线经过坐标原点,且与以A(
| 2 |
∴k=1
∴双曲线的方程为
| y2 |
| 2 |
| x2 |
| 2 |
(2)设过A点的一条直线方程为y=m(x-
| 2 |
代入双曲线方程并化简得(m2-1)x2-2
| 2 |
由题意,
2
| ||
| m2-1 |
|
经验证,满足题意
∴直线方程为y=±
|
| 2 |
点评:本题的考点是直线与圆锥曲线的综合问题,主要考查双曲线标准方程的求解,考查直线与双曲线的位置关系,关键是合理运用双曲线的几何性质,对于是否存在性问题,通常转化为封闭型问题求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,0)为右焦点的双曲线C的离心率,
,0)为右焦点的双曲线C的离心率,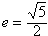 。
。