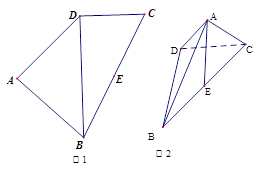
题目内容
(本小题满分10分)已知:四边形ABCD是空间四边形,E, H分别是边AB,AD的中点,F, G分别是边CB,CD上的点,且 .
.
求证:(1)四边形EFGH是梯形;
(2)FE和GH的交点在直线AC上 .
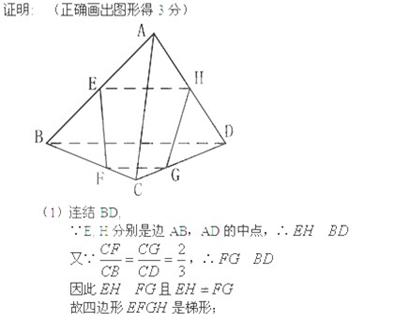 ----------5分
----------5分
(2)由(1)知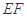 ,
,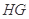 相交,设
相交,设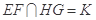
∵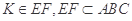 平面,∴
平面,∴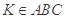 平面 ------------ 7分
平面 ------------ 7分
同理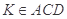 平面,又平面
平面,又平面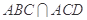 平面
平面
∴ 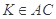 ------------------ 10分
------------------ 10分
故FE和GH的交点在直线AC上.
解析试题分析:(1)根据已知中相似比,得到线线的平行问题,在利用相似比得到长度不等,进而得到证明。
(2)在第一问的基础上,先确定出两条直线有个交点,证明第三条直线过该点即可。
考点:本题主要是考查线线平行的证明以及平面内性质中公理3的运用。
点评:解决该试题的关键是利用一组对边线线平行且边长不等,来证明是否为梯形,同时利用公理三得到线共点问题的证明。

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 中,底面
中,底面 是直角梯形,
是直角梯形, ∥
∥ ,∠
,∠ ,
,  ,平面
,平面 ⊥平面
⊥平面 .
.
 和平面
和平面 所成二面角(小于
所成二面角(小于 )的大小;
)的大小; 上是否存在点
上是否存在点 使得
使得 ∥平面
∥平面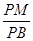 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.  与
与 均为菱形,
均为菱形,  ,且
,且 ,
,
 平面
平面 ;
; 的余弦值。
的余弦值。 ,AB=8,BC=6,点E是PC的中点,F在AD上且AF:FD=1:2.建立适当坐标系.
,AB=8,BC=6,点E是PC的中点,F在AD上且AF:FD=1:2.建立适当坐标系.
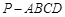 中,
中,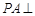 平面
平面 ,
,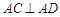 ,
,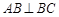 ,
,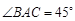 ,
,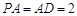 ,
,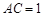 .
.
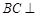 平面
平面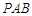
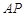 和平面
和平面 所成角的正弦值
所成角的正弦值 的正切值;
的正切值;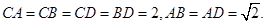

 平面BCD;
平面BCD;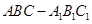 中,
中, ,
,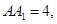 点
点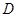 是
是 的中点。
的中点。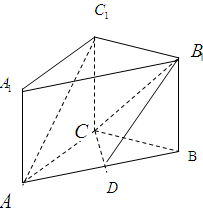

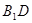 与平面
与平面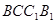 所成的角的正切值
所成的角的正切值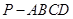 中,
中, 底面
底面 ,四边形
,四边形 ,
, ,
,  ,
, ,E为
,E为 中点.
中点.
 中(图1),
中(图1), 是
是 的中点,
的中点, ,
,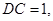
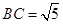 ,
,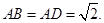 将(图1)沿直线
将(图1)沿直线 折起,使二面角
折起,使二面角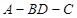 为
为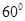 (如图2)
(如图2) 平面
平面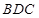 ;
;