题目内容
 已知全集U为实数集R,集合M={x|
已知全集U为实数集R,集合M={x|| x+3 |
| x-1 |
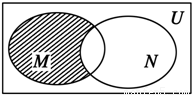
分析:解不等式求得集合M、N,根据Venn图阴影表示集合(CuN)∩M,再进行集合运算.
解答:解:∵
<0⇒-3<x<1∴M=(-3,1),
∵|x|≤1⇒-1≤x≤1,∴N=[-1,1],
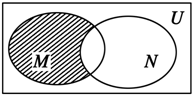
∵阴影部分表示集合(CuN)∩M,
∴阴影部分表示的集合是(-3,-1).
故选D
| x+3 |
| x-1 |
∵|x|≤1⇒-1≤x≤1,∴N=[-1,1],
∵阴影部分表示集合(CuN)∩M,
∴阴影部分表示的集合是(-3,-1).
故选D
点评:本题考查Venn图表达集合的关系及集合运算.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
 <0},N={x||x|≤1},则右图中阴影部分表示的集合是( )
<0},N={x||x|≤1},则右图中阴影部分表示的集合是( ) 已知全集U为实数集R,集合M={x|
已知全集U为实数集R,集合M={x|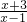 <0},N={x||x|≤1},则如图阴影部分表示的集合是
<0},N={x||x|≤1},则如图阴影部分表示的集合是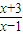 <0},N={x||x|≤1},则如图阴影部分表示的集合是( )
<0},N={x||x|≤1},则如图阴影部分表示的集合是( )