题目内容
设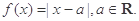
(1)当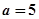 ,解不等式
,解不等式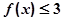 ;
;
(2)当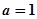 时,若
时,若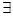
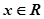 ,使得不等式
,使得不等式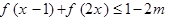 成立,求
成立,求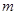 的取值范围.
的取值范围.
(1)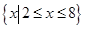 ;(2)
;(2) ﹒
﹒
解析试题分析:(1)当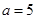 时,不等式
时,不等式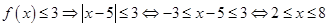 ,故所求不等式的解为
,故所求不等式的解为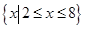 .
.
(2)当 时,由题设得
时,由题设得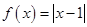 ,则
,则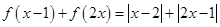 ,构造函数
,构造函数 ,则原不等式可化为
,则原不等式可化为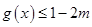 ,只需存在
,只需存在 时不等式成立即可,所以原不等式等价于
时不等式成立即可,所以原不等式等价于 ,而对于函数
,而对于函数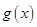 有当
有当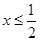 时,
时, 为单调递减函数,此时
为单调递减函数,此时 ;当
;当 时,
时,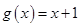 为单调递增函数,此时
为单调递增函数,此时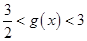 ;当
;当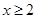 时,
时,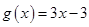 为单调递增函数,此时
为单调递增函数,此时 ,综合得
,综合得 ,所以
,所以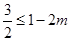 ,解之得
,解之得 .
.
试题解析:(1)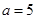 时原不等式等价于
时原不等式等价于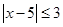 即
即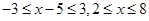 ,
,
所以解集为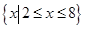 . 5分
. 5分
(2)当 时,
时,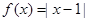 ,令
,令 ,
,
由图像知:当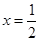 时,
时, 取得最小值
取得最小值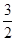 ,由题意知:
,由题意知: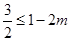 ,
,
所以实数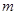 的取值范围为
的取值范围为 . 12分
. 12分
考点:绝对值不等式

练习册系列答案
相关题目
 的不等式
的不等式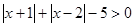 .
.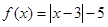 ,
,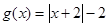 。
。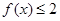 的解集;
的解集;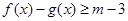 有解,求实数
有解,求实数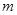 的取值范围。
的取值范围。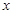 的一元二次不等式
的一元二次不等式 .
.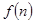 表示,且
表示,且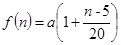 (其中
(其中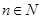 ),又知建5座球场时,每平方米的平均建筑费用为400元.
),又知建5座球场时,每平方米的平均建筑费用为400元.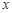 的不等式f(x)≥m2-3m的解集是R,求m的取值范围
的不等式f(x)≥m2-3m的解集是R,求m的取值范围 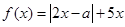 ,其中实数
,其中实数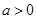 .
.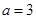 时,求不等式
时,求不等式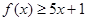 的解集;
的解集;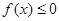 的解集为
的解集为 ,求
,求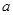 的值.
的值.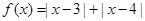 .
.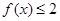 ;
;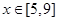 ,
,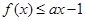 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.