题目内容
已知数列{an}的前n项和为Sn,求数列的通项公式.(1)Sn=2n2+3n;(2)Sn=2n-1;(3)Sn=n2+2n+1.
思路解析:利用Sn和an的关系求解. 解:(1)a1=2×12+3×1=5, 当n≥2时,an=Sn-Sn-1=2n2+3n-[2(n-1)2+3(n-1)]=4n+1. 当n=1时,a1=4×1+1=5成立. 所以,an=4n+1. (2)a1=S1=21-1=1, 当n≥2时,an=Sn-Sn-1=(2n-1)-(2n-1-1)=2n-1. 当n=1时,a1=21-1=1成立. 所以,an=2n-1. (3)a1=S1=12+2×1+1=4, 当n≥2时,an=Sn-Sn-1=(n2+2n+1)-[(n-1)2+2(n-1)+1]=2n+1. 当n=1时,a1=2×1+1=3≠4. 所以,an= 误区警示 本题所体现的是怎样由Sn求数列的通项公式an.在求得n≥2时的an的表达式后要注意验证当n=1时a1是否符合an表达式,若不符合,则应写成如第(3)题中的形式.
![]()
 练习册系列答案
练习册系列答案
期末夺冠满分测评卷系列答案
创新考王完全试卷系列答案


期末100分冲刺卷系列答案

聚能闯关期末复习冲刺卷系列答案
同步测试卷过关冲刺100分系列答案

给力闯关100分系列答案
相关题目
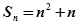 ,那么它的通项公式为an=_________
,那么它的通项公式为an=_________
 ,那么它的通项公式为an=_________
.
,那么它的通项公式为an=_________
. , 则数列的通项an=
, 则数列的通项an=