题目内容
已知数列{an}的前n项和为Sn,a1=
思路解析:先化简递推关系式:n≥2时an=Sn-Sn-1,
∴Sn+![]() +2=Sn-Sn-1,
+2=Sn-Sn-1, ![]() +Sn-1+2=0.
+Sn-1+2=0.
解:当n=1时,S1=a1=![]() .
.
当n=2时,![]() =-2-S1=
=-2-S1=![]() ,∴S2=
,∴S2=![]() .
.
当n=3时,![]() =-2-S2=
=-2-S2=![]() ,∴S3=
,∴S3=![]() .
.
当n=4时,![]() =-2-S3=
=-2-S3=![]() ,∴S4=
,∴S4=![]() .
.
猜想:Sn=![]() (n∈N*).
(n∈N*).
方法规纳 在归纳推理中,所得的结论的正确性常常要用数学归纳法来加以严格证明.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 ,那么它的通项公式为an=_________
,那么它的通项公式为an=_________
 ,那么它的通项公式为an=_________
.
,那么它的通项公式为an=_________
.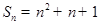 , 则数列的通项an=
, 则数列的通项an=