题目内容
(本小题满分12分)已知 =(2,1),
=(2,1), =(1,7),
=(1,7), =(5,1).设M是直线OP上的一点(其中O为坐标原点),当
=(5,1).设M是直线OP上的一点(其中O为坐标原点),当 取最小值时:
取最小值时:
(1)求 ;
;
(2)设∠AMB=θ,求cosθ的值.
 =(2,1),
=(2,1), =(1,7),
=(1,7), =(5,1).设M是直线OP上的一点(其中O为坐标原点),当
=(5,1).设M是直线OP上的一点(其中O为坐标原点),当 取最小值时:
取最小值时:(1)求
 ;
;(2)设∠AMB=θ,求cosθ的值.
(1)t=2时, 最小,这时
最小,这时 =(4,2).(2)
=(4,2).(2)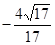 .
.
 最小,这时
最小,这时 =(4,2).(2)
=(4,2).(2)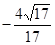 .
.本试题主要是考查了向量的共线的运用,以及向量的数量积公式的运用,求解三角方程。
(1) =t
=t ,则
,则 =(2t,t),
=(2t,t),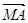 =(1-2t,7-t),
=(1-2t,7-t),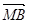 =(5-2t,1-t).
=(5-2t,1-t).
,利用 =5t2-20t+12=5(t-2)2-8.
=5t2-20t+12=5(t-2)2-8.
取得最小值时的t的值得到结论。
(2)由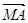 =(-3,5),
=(-3,5),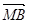 =(1,-1),结合向量的数量积公式得到角的值。
=(1,-1),结合向量的数量积公式得到角的值。
解:设 =t
=t ,则
,则 =(2t,t),
=(2t,t),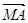 =(1-2t,7-t),
=(1-2t,7-t),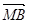 =(5-2t,1-t).
=(5-2t,1-t).
 =5t2-20t+12=5(t-2)2-8.
=5t2-20t+12=5(t-2)2-8.
∴t=2时, 最小,这时
最小,这时 =(4,2).
=(4,2).
(2)由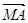 =(-3,5),
=(-3,5),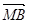 =(1,-1),
=(1,-1),
∴cosθ=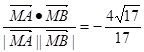 .
.
∴cosθ的值是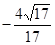 .
.
(1)
 =t
=t ,则
,则 =(2t,t),
=(2t,t),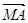 =(1-2t,7-t),
=(1-2t,7-t),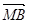 =(5-2t,1-t).
=(5-2t,1-t).,利用
 =5t2-20t+12=5(t-2)2-8.
=5t2-20t+12=5(t-2)2-8.取得最小值时的t的值得到结论。
(2)由
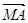 =(-3,5),
=(-3,5),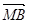 =(1,-1),结合向量的数量积公式得到角的值。
=(1,-1),结合向量的数量积公式得到角的值。解:设
 =t
=t ,则
,则 =(2t,t),
=(2t,t),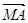 =(1-2t,7-t),
=(1-2t,7-t),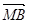 =(5-2t,1-t).
=(5-2t,1-t). =5t2-20t+12=5(t-2)2-8.
=5t2-20t+12=5(t-2)2-8.∴t=2时,
 最小,这时
最小,这时 =(4,2).
=(4,2).(2)由
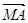 =(-3,5),
=(-3,5),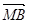 =(1,-1),
=(1,-1),∴cosθ=
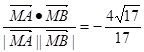 .
.∴cosθ的值是
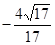 .
.
练习册系列答案
相关题目
 ,若
,若 ,则
,则 ________。
________。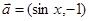
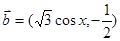 ,函数
,函数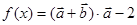
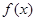 的值域;
的值域;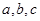 分别为△ABC内角A,B,C的对边,
分别为△ABC内角A,B,C的对边,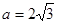 ,且
,且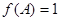 ,求A和△ABC面积的最大值。
,求A和△ABC面积的最大值。 若
若 与
与 平行,则实数
平行,则实数 的值是( )
的值是( ) 中,已知
中,已知 ∥
∥ ,
, ,
, ,
, ,
, ,若
,若 为
为 的中点,则
的中点,则 的值为
的值为



 若A、B、C三点共线,
若A、B、C三点共线,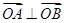 ,求
,求 的值.
的值.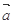 =(
=(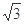 ,1),
,1),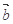 =(0,-1),
=(0,-1),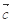 =(k,
=(k,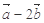 与
与 且A(
且A(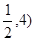 ,B(
,B( ,则
,则 ( )
( )

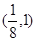

 ,
, ,向量
,向量 ,
, ,
, 且
且 ,
, ,则
,则 .
.