题目内容
已知向量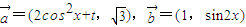 ,函数f(x)=
,函数f(x)=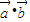 .
.(1)求函数y=f(x)的最小正周期以及单调递增区间;
(2)当
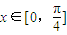 时,f(x)有最大值4,求实数t的值.
时,f(x)有最大值4,求实数t的值.
【答案】分析:(1)利用三角函数的恒等变换化简函数f(x)的解析式为 2sin(2x+ )+t+1,由此求出它的周期,再由 2kπ-
)+t+1,由此求出它的周期,再由 2kπ-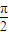 ≤2x+
≤2x+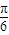 ≤2kπ+
≤2kπ+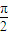 ,k∈z,求出x的范围,即可求得函数的单调递增区间.
,k∈z,求出x的范围,即可求得函数的单调递增区间.
(2)当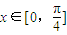 时,
时,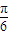 ≤2x+
≤2x+ ≤
≤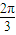 ,1≤2sin(2x+
,1≤2sin(2x+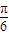 )≤2,由此求得t+2≤f(x)≤t+3,再由最大值为4,可得 t+3=4,从而求得t的值.
)≤2,由此求得t+2≤f(x)≤t+3,再由最大值为4,可得 t+3=4,从而求得t的值.
解答:解:(1)函数f(x)=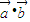 =2cos2x+t+
=2cos2x+t+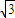 sin2x=1=cos2x+1+t+
sin2x=1=cos2x+1+t+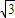 sin2x=2sin(2x+
sin2x=2sin(2x+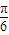 )+t+1.
)+t+1.
故它的最小正周期为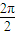 =π.
=π.
令 2kπ-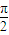 ≤2x+
≤2x+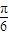 ≤2kπ+
≤2kπ+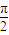 ,k∈z,可得 kπ-
,k∈z,可得 kπ-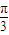 ≤x≤kπ+
≤x≤kπ+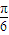 ,
,
故函数的单调递增区间为[kπ-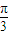 ,kπ+
,kπ+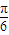 ],k∈z.
],k∈z.
(2)当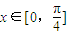 时,
时,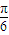 ≤2x+
≤2x+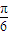 ≤
≤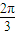 ,∴1≤2sin(2x+
,∴1≤2sin(2x+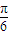 )≤2,
)≤2,
∴t+2≤f(x)≤t+3.
由于(x)有最大值4,故 t+3=4,t=1.
点评:本题主要考查两个向量数量积公式,三角函数的恒等变换及化简求值,复合三角函数的单调性,三角函数的周期性和求法,属于中档题.
 )+t+1,由此求出它的周期,再由 2kπ-
)+t+1,由此求出它的周期,再由 2kπ-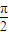 ≤2x+
≤2x+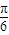 ≤2kπ+
≤2kπ+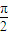 ,k∈z,求出x的范围,即可求得函数的单调递增区间.
,k∈z,求出x的范围,即可求得函数的单调递增区间.(2)当
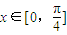 时,
时,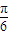 ≤2x+
≤2x+ ≤
≤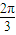 ,1≤2sin(2x+
,1≤2sin(2x+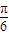 )≤2,由此求得t+2≤f(x)≤t+3,再由最大值为4,可得 t+3=4,从而求得t的值.
)≤2,由此求得t+2≤f(x)≤t+3,再由最大值为4,可得 t+3=4,从而求得t的值.解答:解:(1)函数f(x)=
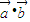 =2cos2x+t+
=2cos2x+t+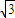 sin2x=1=cos2x+1+t+
sin2x=1=cos2x+1+t+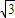 sin2x=2sin(2x+
sin2x=2sin(2x+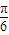 )+t+1.
)+t+1.故它的最小正周期为
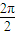 =π.
=π.令 2kπ-
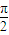 ≤2x+
≤2x+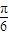 ≤2kπ+
≤2kπ+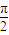 ,k∈z,可得 kπ-
,k∈z,可得 kπ-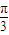 ≤x≤kπ+
≤x≤kπ+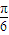 ,
,故函数的单调递增区间为[kπ-
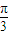 ,kπ+
,kπ+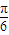 ],k∈z.
],k∈z.(2)当
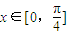 时,
时,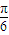 ≤2x+
≤2x+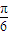 ≤
≤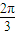 ,∴1≤2sin(2x+
,∴1≤2sin(2x+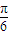 )≤2,
)≤2,∴t+2≤f(x)≤t+3.
由于(x)有最大值4,故 t+3=4,t=1.
点评:本题主要考查两个向量数量积公式,三角函数的恒等变换及化简求值,复合三角函数的单调性,三角函数的周期性和求法,属于中档题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
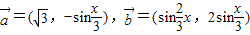 ,函数f(x)=
,函数f(x)=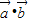 .
.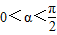 且
且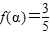 ,求
,求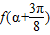 的值.
的值.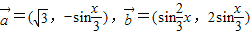 ,函数f(x)=
,函数f(x)=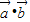 .
.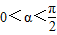 且
且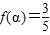 ,求
,求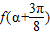 的值.
的值.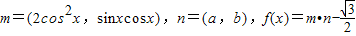 ,函数f(x)的图象关于直线
,函数f(x)的图象关于直线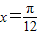 对称,且
对称,且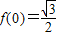
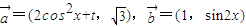 ,函数f(x)=
,函数f(x)=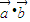 .
.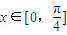 时,f(x)有最大值4,求实数t的值.
时,f(x)有最大值4,求实数t的值.