题目内容
某高中有高级教师96人,中级教师144人,初级教师48人,为了进一步推进高中课程改革,邀请甲、乙、丙、丁四位专家到校指导.学校计划从所有教师中采用分层抽样办法选取6名教师分别与专家一对一交流,选出的6名教师再由专家随机抽取教师进行教学调研,每位教师只与其中一位专家交流一次,每位专家至少与一名教师交流.
(1)求应从高级教师、中级教师、初级教师中分别抽取几人;
(2)若甲专家选取了两名教师,这两名教师分别是高级教师和中级教师的概率;
(3)求高级教师不被同一专家抽取到的概率.
(1)求应从高级教师、中级教师、初级教师中分别抽取几人;
(2)若甲专家选取了两名教师,这两名教师分别是高级教师和中级教师的概率;
(3)求高级教师不被同一专家抽取到的概率.
分析:(1)先求出每位教师被抽到的概率,再用每层的教师数乘以每位教师被抽到的概率,即得应从每层教师中抽取的人数;
(2)列举出甲专家选取了两名教师的所有可能的结果,再得到“甲抽取到一名高级教师和一名中级教师”的可能结果,直接利用古典概型的概率计算公式计算;
(3)列举出两名高级教师所有被抽取情况总数,再得到“两名高级教师不被同一名专家抽到”的可能结果数,直接利用古典概型的概率计算公式计算.
(2)列举出甲专家选取了两名教师的所有可能的结果,再得到“甲抽取到一名高级教师和一名中级教师”的可能结果,直接利用古典概型的概率计算公式计算;
(3)列举出两名高级教师所有被抽取情况总数,再得到“两名高级教师不被同一名专家抽到”的可能结果数,直接利用古典概型的概率计算公式计算.
解答: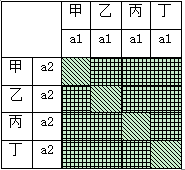 解:(1)从高级教师、中级教师、初级教师中分别抽数目之比为:96:144:48=2:3:1
解:(1)从高级教师、中级教师、初级教师中分别抽数目之比为:96:144:48=2:3:1
得:从高级教师、中级教师、初级教师中分别抽数目分别为2,3,1.
(2)设抽取的6人中高级教师为a1、a2,中级教师为b1、b2、b3,初级教师为c1;
则甲抽取2两名教师所有可能的结果为:(a1,a2),(a1,b1),(a1,b2)(a1,b3),(a1,c1),
(a2,b1),(a2,b2),(a2,b3),(a2,c1),
(b1,b2),(b1,b3),(b1,c1),(b2,b3),(b2,c1),(b3,c1)共15种;
其中甲抽取到一名高级教师和一名中级教师结果为:(a1,b1),(a1,b2)(a1,b3),
(a2,b1),(a2,b2),(a2,b3)共6种
所以甲抽取到一名高级教师和一名中级教师的概率为
=
.
(3)两名高级教师所有被抽取情况如下表,每一个阴影部分代表一种分配情况,共有16种,
但是两名高级教师不被同一名专家抽到的情况为网格部分,共有12种情况,
所以两名高级教师不被同一专家抽取到的概率
=
.
 解:(1)从高级教师、中级教师、初级教师中分别抽数目之比为:96:144:48=2:3:1
解:(1)从高级教师、中级教师、初级教师中分别抽数目之比为:96:144:48=2:3:1得:从高级教师、中级教师、初级教师中分别抽数目分别为2,3,1.
(2)设抽取的6人中高级教师为a1、a2,中级教师为b1、b2、b3,初级教师为c1;
则甲抽取2两名教师所有可能的结果为:(a1,a2),(a1,b1),(a1,b2)(a1,b3),(a1,c1),
(a2,b1),(a2,b2),(a2,b3),(a2,c1),
(b1,b2),(b1,b3),(b1,c1),(b2,b3),(b2,c1),(b3,c1)共15种;
其中甲抽取到一名高级教师和一名中级教师结果为:(a1,b1),(a1,b2)(a1,b3),
(a2,b1),(a2,b2),(a2,b3)共6种
所以甲抽取到一名高级教师和一名中级教师的概率为
| 6 |
| 15 |
| 2 |
| 5 |
(3)两名高级教师所有被抽取情况如下表,每一个阴影部分代表一种分配情况,共有16种,
但是两名高级教师不被同一名专家抽到的情况为网格部分,共有12种情况,
所以两名高级教师不被同一专家抽取到的概率
| 12 |
| 16 |
| 3 |
| 4 |
点评:本题考查了列举法计算基本事件数及事件发生的概率,解答此题的关键是列举时做到不重不漏,是中档题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目