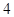题目内容
15、设是空间的三条直线,给出以下五个命题:
①若a⊥b,b⊥c,则a⊥c;
②若a、b是异面直线,b、c是异面直线,则a、c也是异面直线;
③若a和b相交,b和c相交,则a和c也相交;
④若a和b共面,b和c共面,则a和c也共面;
⑤若a∥b,b∥c,则a∥c;
其中正确的命题的序号是
①若a⊥b,b⊥c,则a⊥c;
②若a、b是异面直线,b、c是异面直线,则a、c也是异面直线;
③若a和b相交,b和c相交,则a和c也相交;
④若a和b共面,b和c共面,则a和c也共面;
⑤若a∥b,b∥c,则a∥c;
其中正确的命题的序号是
⑤
.分析:本题考查平面的基本性质,对5个选项逐一进行判断,可以得到正确的结论.
解答:解:①不妨令a与c相交共面α,则b⊥α,a与c相交但不一定垂直,因此①不对;
②若a、b是异面直线,b、c是异面直线,则a、c也可以平行,故②不对;
③不妨令a,b,c共面α且a∥c,即可判断③不对;
④若a和b共面,b和c共面,则a和c可以共面也可以异面,故④不对;
⑤若a若a∥b,b∥c,则a∥c,这是课本上的公理四,正确.
故答案为:⑤
②若a、b是异面直线,b、c是异面直线,则a、c也可以平行,故②不对;
③不妨令a,b,c共面α且a∥c,即可判断③不对;
④若a和b共面,b和c共面,则a和c可以共面也可以异面,故④不对;
⑤若a若a∥b,b∥c,则a∥c,这是课本上的公理四,正确.
故答案为:⑤
点评:本题考查平面的基本性质,考查空间想象能力,方法是借助图形分析.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 是三条直线,若
是三条直线,若 ,则
,则 ∥
∥ ”,得出如下结论:
”,得出如下结论: 是两条直线,
是两条直线,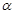 是平面,若
是平面,若 ,则
,则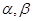 是两个平面,
是两个平面,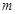 是直线,若
是直线,若 则
则 ;
;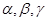 是三个平面,若
是三个平面,若 ,则
,则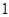 B.
B. C.
C. D.
D.