题目内容
对于正项数列{an},定义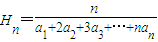 为{an}的“光阴”值,现知某数列的“光阴”值为
为{an}的“光阴”值,现知某数列的“光阴”值为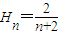 ,则数列{an}的通项公式为 .
,则数列{an}的通项公式为 .
【答案】分析:根据“光阴”值的定义,及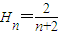 ,可得a1+2a2+…+nan=
,可得a1+2a2+…+nan=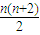 ,再写一式,两式相减,即可得到结论.
,再写一式,两式相减,即可得到结论.
解答:解:∵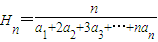
∴a1+2a2+…+nan=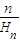
∵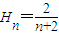
∴a1+2a2+…+nan=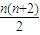 ①
①
∴a1+2a2+…+(n-1)an-1=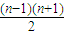 ②
②
①-②得 -
-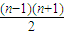 =
=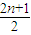
∴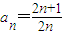
故答案为: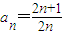
点评:本题考查新定义,考查数列的通项,解题的关键是理解新定义,通过再写一式,两式相减得到结论.
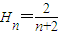 ,可得a1+2a2+…+nan=
,可得a1+2a2+…+nan=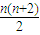 ,再写一式,两式相减,即可得到结论.
,再写一式,两式相减,即可得到结论.解答:解:∵
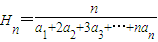
∴a1+2a2+…+nan=
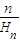
∵
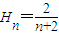
∴a1+2a2+…+nan=
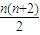 ①
①∴a1+2a2+…+(n-1)an-1=
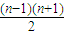 ②
②①-②得
 -
-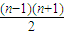 =
=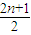
∴
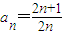
故答案为:
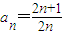
点评:本题考查新定义,考查数列的通项,解题的关键是理解新定义,通过再写一式,两式相减得到结论.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
相关题目
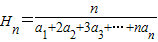 为{an}的“光阴”值,现知某数列的“光阴”值为
为{an}的“光阴”值,现知某数列的“光阴”值为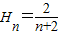 ,则数列{an}的通项公式为 .
,则数列{an}的通项公式为 .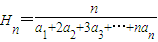 为{an}的“光阴”值,现知某数列的“光阴”值为
为{an}的“光阴”值,现知某数列的“光阴”值为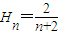 ,则数列{an}的通项公式为 .
,则数列{an}的通项公式为 .