题目内容
如图所示的等腰梯形是一个简易水槽的横断面,已知水槽的最大流量与横断面的面积成正比,比例系数为k(k>0).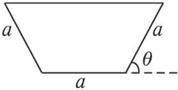
(1)试将水槽的最大流量表示成关于θ的函数f(θ);
(2)求当θ多大时,水槽的流量最大?
解:(1)设水槽的截面面积为S,则S=![]() [a+(a+2acosθ)]·asinθ=a2sinθ(1+cosθ),
[a+(a+2acosθ)]·asinθ=a2sinθ(1+cosθ),
则f(θ)=kS=a2ksinθ(1+cosθ),θ∈(0,![]() ).
).
注:若遗漏系数k,
(2)因为f′(θ)=a2k(2cos2θ+cosθ-1),令f′(θ)=0,则2cos2θ+cosθ-1=0,
解得cosθ=![]() 或cosθ=-1.
或cosθ=-1.
由于0<θ<![]() ,得cosθ≠-1,所以cosθ=
,得cosθ≠-1,所以cosθ=![]() ,此时θ=
,此时θ=![]() .
.
因为0<θ<![]() 时,f′(θ)>0;
时,f′(θ)>0;![]() <θ<
<θ<![]() 时,f′(θ)<0,
时,f′(θ)<0,
所以,当θ=![]() 时,水槽的流量最大.
时,水槽的流量最大.
注:若转化为多项式函数求最值的,仿此给分.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 如图所示的等腰梯形是一个简易水槽的横断面,已知水槽的最大流量与横断面的面积成正比,比例系数为k(k>0).当θ=
如图所示的等腰梯形是一个简易水槽的横断面,已知水槽的最大流量与横断面的面积成正比,比例系数为k(k>0).当θ=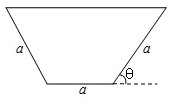 如图所示的等腰梯形是一个简易水槽的横断面,已知水槽的最大流量与横断面的面积成正比,比例系数为k(k>0).
如图所示的等腰梯形是一个简易水槽的横断面,已知水槽的最大流量与横断面的面积成正比,比例系数为k(k>0).
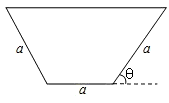 如图所示的等腰梯形是一个简易水槽的横断面,已知水槽的最大流量与横断面的面积成正比,比例系数为k(k>0).
如图所示的等腰梯形是一个简易水槽的横断面,已知水槽的最大流量与横断面的面积成正比,比例系数为k(k>0).