题目内容
已知sin2θ=a,cos2θ=b,0<θ<
,给出tan(θ+
)值的五个答案:①
;②
;③
;④
; ⑤
.其中正确的是( )
| π |
| 4 |
| π |
| 4 |
| b |
| 1-a |
| a |
| 1-b |
| 1+b |
| a |
| 1+a |
| b |
| a-b+1 |
| a+b-1 |
分析:由题词设条件,可对tan(θ+
)的形式进行了探究,得出其用sin2θ=a,cos2θ=b的表达式,从而得出它的答案的形式,选出正确选项,
| π |
| 4 |
解答:解:∵tan(θ+
)=
=
=
=
=
∴①④是正确的
考察四个选项,只有C符合,将sin2θ=a,cos2θ=b代入⑤验证知,此代数式也是正确的答案
故选C
| π |
| 4 |
| sinθ+cosθ |
| cosθ-sinθ |
| 1+sin2θ |
| cos2θ |
| cos2θ |
| 1-sin2θ |
| b |
| 1-a |
| 1+a |
| b |
∴①④是正确的
考察四个选项,只有C符合,将sin2θ=a,cos2θ=b代入⑤验证知,此代数式也是正确的答案
故选C
点评:本题考查了两角和与差的正切函数,正弦、余弦的二倍角公式,解题的关键是掌握公式且能根据公式进行灵活变形从而解出答案的不同形式,本题的难点是探究答案的不同形式,由于答案表示方法不唯一,本题是一个开放式题,解本题时由于①④两个结论易证明,且四个选项中仅有C同时包含①④,故解本题时注意到这一情况,则没有必要再验证⑤的成立与否,这将大大降低计算量.

练习册系列答案
相关题目
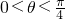 ,给出
,给出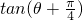 值的五个答案:①
值的五个答案:①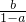 ;②
;② ;③
;③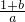 ;④
;④ ; ⑤
; ⑤ .其中正确的是
.其中正确的是