题目内容
 某中学高二级某班一个户外小组搞野炊活动,其中要购买A,B两种蔬菜,A、B蔬菜每斤的单价分别为2元和3 元.根据需要,A蔬菜至少要买6斤,B蔬菜至少要买4斤,而且购买这两种蔬菜的总费用不能超过60元.
某中学高二级某班一个户外小组搞野炊活动,其中要购买A,B两种蔬菜,A、B蔬菜每斤的单价分别为2元和3 元.根据需要,A蔬菜至少要买6斤,B蔬菜至少要买4斤,而且购买这两种蔬菜的总费用不能超过60元.(1)写出活动中A蔬菜购买的斤数x和B蔬菜购买的斤数y之间的不等式组;
(2)在下面给定的坐标系中画出(1)中不等式组表示的平面区域(用阴影表示),并求出它的面积.
分析:(1)设活动中A蔬菜购买的斤数为x斤,B蔬菜购买的斤数为y斤,根据A、B蔬菜每斤的单价分别为2元和3 元.根据需要,A蔬菜至少要买6斤,B蔬菜至少要买4斤,而且购买这两种蔬菜的总费用不能超过60元,易得到活动中A蔬菜购买的斤数x和B蔬菜购买的斤数y之间的不等式组;
(2)根据二元一次不等式与对应平面区域的关系,我们易画出(1)中不等式组对应的平面区域,根据区域的各个角点坐标,我们判断出其形状及边长,代入面积公式,即可得到答案.
(2)根据二元一次不等式与对应平面区域的关系,我们易画出(1)中不等式组对应的平面区域,根据区域的各个角点坐标,我们判断出其形状及边长,代入面积公式,即可得到答案.
解答: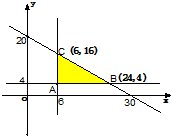 解:设活动中A蔬菜购买的斤数为x斤,B蔬菜购买的斤数为y斤,…(1分)
解:设活动中A蔬菜购买的斤数为x斤,B蔬菜购买的斤数为y斤,…(1分)
则:(1)
…(4分)
(2)画出的平面区域如右图,…(7分)
易得A(6,4),…(8分)
由
求得C(6,16)…(10分)
由
求得B(24,4)…(12分)
∴s△ABC=
AB•AC=
×18×12=108…(14分)
 解:设活动中A蔬菜购买的斤数为x斤,B蔬菜购买的斤数为y斤,…(1分)
解:设活动中A蔬菜购买的斤数为x斤,B蔬菜购买的斤数为y斤,…(1分)则:(1)
|
(2)画出的平面区域如右图,…(7分)
易得A(6,4),…(8分)
由
|
由
|
∴s△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的知识点是不等式关系与不等式,简单线性规划,其中根据已知条件建立不等式组,将一个实际问题转化为一个数学模型是解答本题的关键.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 某中学高二级某班一个户外小组搞野炊活动,其中要购买A,B两种蔬菜,A、B蔬菜每斤的单价分别为2元和3 元.根据需要,A蔬菜至少要买6斤,B蔬菜至少要买4斤,而且购买这两种蔬菜的总费用不能超过60元.
某中学高二级某班一个户外小组搞野炊活动,其中要购买A,B两种蔬菜,A、B蔬菜每斤的单价分别为2元和3 元.根据需要,A蔬菜至少要买6斤,B蔬菜至少要买4斤,而且购买这两种蔬菜的总费用不能超过60元.