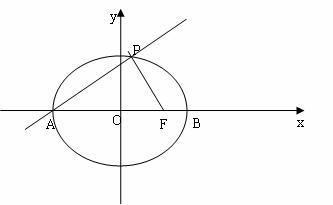
题目内容
(本题13分)已知椭圆![]() 的方程是
的方程是![]()
![]() ,点
,点![]() 分别是椭圆的长轴的左、右端点,
分别是椭圆的长轴的左、右端点,
左焦点坐标为![]() ,且过点
,且过点![]() 。
。
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知![]() 是椭圆
是椭圆![]() 的右焦点,以
的右焦点,以![]() 为直径的圆记为圆
为直径的圆记为圆![]() ,试问:过
,试问:过![]() 点能否引圆
点能否引圆![]() 的切线,若能,求出这条切线与
的切线,若能,求出这条切线与![]() 轴及圆
轴及圆![]() 的弦
的弦![]() 所对的劣弧围成的图形的面积;若不能,说明理由。
所对的劣弧围成的图形的面积;若不能,说明理由。
【解析】(Ⅰ)因为椭圆![]() 的方程为
的方程为![]() ,(
,(![]() ), ∴
), ∴ ![]() ,
,
即椭圆的方程为![]() , ∵ 点
, ∵ 点![]() 在椭圆上, ∴
在椭圆上, ∴ ![]() ,
,
解得 ![]() 或
或![]() (舍), 由此得
(舍), 由此得![]() ,
,
所以,所求椭圆![]() 的标准方程为
的标准方程为![]() . …… 6分
. …… 6分
(Ⅱ)由(Ⅰ)知![]() ,
,![]() ,又
,又![]() ,则得
,则得
![]() ,
,![]()
所以![]() ,即
,即![]() ,
, ![]() 是
是![]() ,
,
所以,以![]() 为直径的圆
为直径的圆![]() 必过点
必过点![]() ,
,
因此,过![]() 点能引出该圆
点能引出该圆![]() 的切线,
的切线,
设切线为![]() ,交
,交![]() 轴于
轴于![]() 点,
点,
又![]() 的中点为
的中点为![]() ,则显然
,则显然![]() ,
,
而  ,
,
所以![]() 的斜率为
的斜率为![]() ,
,
因此,过![]() 点引圆
点引圆![]() 的切线方程为:
的切线方程为: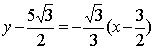 ,
,
即![]()
令![]() ,则
,则![]() ,
,![]() ,又
,又![]() ,
,
所以![]() ,
,
![]() 因此,所求的图形面积是
因此,所求的图形面积是 ![]() =
=![]()
![]()
![]() …… 13分
…… 13分


练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
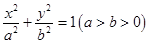 的离心率
的离心率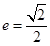 ,短轴长为
,短轴长为
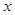 轴正半轴、
轴正半轴、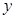 轴正半轴的交点分别为
轴正半轴的交点分别为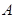 、
、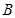 ,经过点
,经过点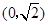 且斜率k的直线
且斜率k的直线 与椭圆交于不同的两点
与椭圆交于不同的两点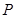 、
、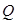 ,是否存在常数
,是否存在常数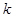 ,使得向量
,使得向量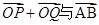 共线?如果存在,求
共线?如果存在,求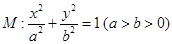 的左右焦点分别为
的左右焦点分别为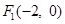 ,
,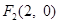 .在椭圆
.在椭圆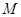 中有一内接三角形
中有一内接三角形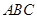 ,其顶点
,其顶点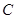 的坐标
的坐标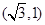 ,
,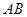 所在直线的斜率为
所在直线的斜率为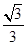 .
. 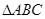 的面积最大时,求直线
的面积最大时,求直线
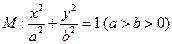 的左右焦点分别
的左右焦点分别 为
为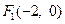 ,
,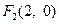 .在椭圆
.在椭圆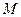 中有一内接三角形
中有一内接三角形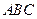 ,其顶点
,其顶点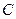 的坐
的坐 标
标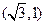 ,
,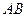 所在直线的斜率为
所在直线的斜率为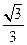 .
.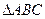 的面积最大时,求直线
的面积最大时,求直线