题目内容
若a=2,求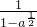 +
+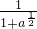 +
+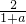 的值.
的值.
解:原式=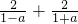 =
=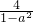 ,
,
∵a=2,
∴原式=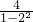 =-
=- .
.
分析:利用指数幂的运算法则通分化简即可.
点评:熟练掌握指数幂的运算性质是解题的关键.
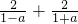 =
=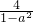 ,
,∵a=2,
∴原式=
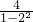 =-
=- .
.分析:利用指数幂的运算法则通分化简即可.
点评:熟练掌握指数幂的运算性质是解题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
题目内容
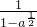 +
+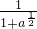 +
+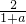 的值.
的值.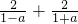 =
=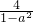 ,
,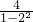 =-
=- .
.
 优生乐园系列答案
优生乐园系列答案