Question

已知X～N（-1，σ²），若P（X≤-3）=0.2，则P（-3≤X≤1）=

0.6

．

Answer 1

分析：观察正态曲线得，根据对称性，由图可得，P（-3≤x≤1）=0.6．

解答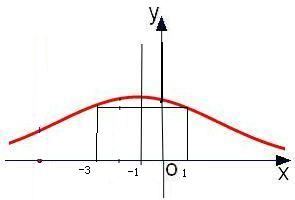：解：画出正态曲线，根据对称性，由图可得，
若P（X≤-3）=0.2，得P（X≥1）=0.2，
从而P（-3≤x≤1）=1-2P（X≥1）=0.6．
故答案为：0.6．

点评：本题考查正态分布中概率的求法，图中μ就是数学期望．它恰好是曲线最高点的横坐标，直线 就是曲线的对称轴，可见μ决定了正态分布密度曲线的位置．随机变量X的大部分的值都集中在μ的附近，从曲线的图形可以直观地看出随机变量的这个特征．