题目内容
设指数函数y=ax与对数函数y=logax(a>0,a≠1)的图象分别为C1,C2,点M在曲线C1上,线段OM(O为坐标原点)交曲线C1于另一点N.若曲线C2上存在一点P,使点P的横坐标与点M的纵坐标相等,点P的纵坐标是点N的横坐标的2倍,则点P的坐标是( )
分析:设P(m,logam),可设M(α,m),N(
logam,β),根据曲线C1、C2的表达式,解出α=logam,β=
,得出M、N坐标关于a、m的表达形式,最后根据M、N、O三点共线,利用斜率相等建立关系式可得出m=4,从而得出点P的坐标.
| 1 |
| 2 |
| m |
解答:解:设P(m,logam),则可设M(α,m),N(
logam,β)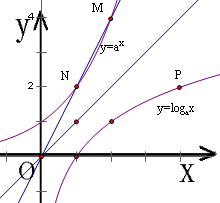
∵M(α,m),N(
logam,β)在指数函数y=ax的图象上
∴m=aα且β=a
logam,解之得α=logam,β=
由此可得M(logam,m),N(
logam,
)
∵M、N、O三点共线
∴kOM=KON,即
=
,解之得m=4(舍去0)
因此点P的坐标为(4,logam)
故选:C
| 1 |
| 2 |

∵M(α,m),N(
| 1 |
| 2 |
∴m=aα且β=a
| 1 |
| 2 |
| m |
由此可得M(logam,m),N(
| 1 |
| 2 |
| m |
∵M、N、O三点共线
∴kOM=KON,即
| m |
| logam |
| ||
|
因此点P的坐标为(4,logam)
故选:C
点评:本题给出指数函数和对数函数图象上点坐标之间的关系,求其中一个点的坐标,着重考查了函数的图象与性质、指数和对数函数图象与性质的综合应用等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目