题目内容
已知数列 为等差数列,若
为等差数列,若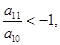 且它们的前
且它们的前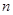 项和
项和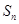 有最大值,则使得
有最大值,则使得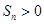 的
的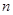 的最大值为( )
的最大值为( )
| A.11 | B.19 | C.20 | D.21 |
B
解析试题分析:根据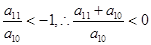 ,由它们的前n项和Sn有最大可得数列的d<0,∴a10>0,a11+a10<0,a11<0,∴a1+a19=2a10>0,a1+a20=a11+a10<0,使得Sn>0的n的最大值n=19,故选B
,由它们的前n项和Sn有最大可得数列的d<0,∴a10>0,a11+a10<0,a11<0,∴a1+a19=2a10>0,a1+a20=a11+a10<0,使得Sn>0的n的最大值n=19,故选B
考点:本题主要考查了考查了等差数列的性质在求解和的最值中应用.
点评:解题的关键是由已知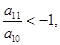 及它们的前n项和Sn有最大,a10>0,a11+a10<0,a11<0,灵活利用和公式及等差数列的性质得到a1+a19=2a10>0,a1+a20=a11+a10<0是解决本题的另外关键点.
及它们的前n项和Sn有最大,a10>0,a11+a10<0,a11<0,灵活利用和公式及等差数列的性质得到a1+a19=2a10>0,a1+a20=a11+a10<0是解决本题的另外关键点.

练习册系列答案
相关题目
已知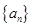 是等差数列,
是等差数列,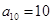 ,其前10项和
,其前10项和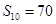 ,则其公差
,则其公差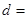 ( )
( )
A.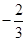 | B.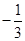 | C. | D.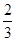 |
等差数列{an}的前n项和为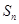 .已知
.已知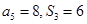 ,则
,则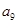 = ( )
= ( )
| A.8 | B.12 | C.16 | D.24 |
已知等差数列 中,
中,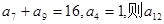 的值是( )
的值是( )
| A.15 | B.30 | C.31 | D.64 |
在等差数列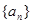 中,
中,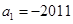 ,前n项和为
,前n项和为 ,且
,且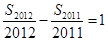 ,则
,则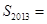
A.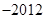 | B.2012 | C.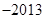 | D.2013 |
已知等差数列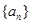 ,
, 则它的公差是( )
则它的公差是( )
| A.1 | B.2 | C.3 | D.4 |
若△ABC的三个内角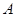 、
、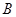 、
、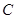 成等差数列,则
成等差数列,则
A.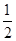 | B.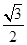 | C.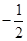 | D.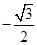 |
已知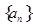 是等差数列,且a2+ a5+ a8+ a11=48,则a6+ a7= ( )
是等差数列,且a2+ a5+ a8+ a11=48,则a6+ a7= ( )
| A.12 | B.16 | C.20 | D.24 |
观察下列各式: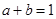 ,
,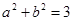 ,
,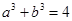 ,
,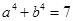 ,
,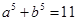 ,
,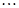 则
则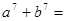 ( )
( )
| A.18 | B.19 | C.29 | D.30 |