题目内容
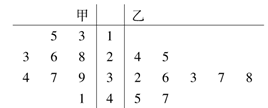
如图所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中的数学成绩.乙组记录中有一个数据模糊,无法确认,在图中以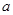 表示.已知甲、乙两个小组的数学成绩的平均分相同.
表示.已知甲、乙两个小组的数学成绩的平均分相同.
(1)求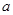 的值;
的值;
(2)求乙组四名同学数学成绩的方差;
(3)分别从甲、乙两组同学中各随机选取一名同学,求这两名同学数学成绩之差的绝对值为3的概率.
(注:方差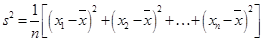 ,其中
,其中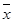 为
为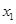 ,
,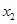 ,…,
,…, 的平均数)
的平均数)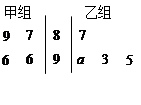
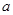 表示.已知甲、乙两个小组的数学成绩的平均分相同.
表示.已知甲、乙两个小组的数学成绩的平均分相同.(1)求
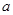 的值;
的值;(2)求乙组四名同学数学成绩的方差;
(3)分别从甲、乙两组同学中各随机选取一名同学,求这两名同学数学成绩之差的绝对值为3的概率.
(注:方差
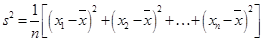 ,其中
,其中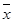 为
为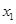 ,
,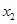 ,…,
,…, 的平均数)
的平均数)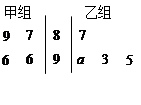
(1)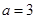 .
.
(2)两组同学数学成绩的平均分都为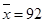 . 乙组四名同学数学成绩的方差为
. 乙组四名同学数学成绩的方差为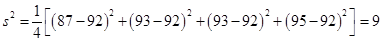 .
.
(3)P(A)=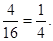
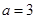 .
.(2)两组同学数学成绩的平均分都为
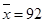 . 乙组四名同学数学成绩的方差为
. 乙组四名同学数学成绩的方差为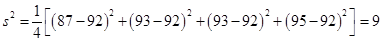 .
. (3)P(A)=
(1)根据甲、乙两组的平均分相同可建立关于a的方程,解出a的值.
(2)先求出平均分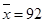 ,然后再利用方差公式计算
,然后再利用方差公式计算
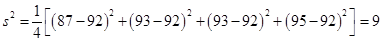 .
.
(3)本小题属于古典概型概率问题,先求出从甲、乙两组同学中各随机选取一名同学,共有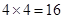 种可能的结果.然后再求出两名同学成绩之差的绝对值为3包含4种可能的结果,
种可能的结果.然后再求出两名同学成绩之差的绝对值为3包含4种可能的结果,
所以所求概率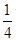 .
.
解:(1)依题意,得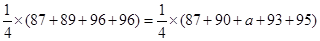 ,……2分
,……2分
解得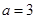 .………………………………………………………………………4分
.………………………………………………………………………4分
(2)根据已知条件,可以求得两组同学数学成绩的平均分都为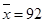 .……………………………5分
.……………………………5分
所以乙组四名同学数学成绩的方差为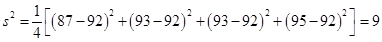 .……………8分
.……………8分
(3)分别从甲、乙两组同学中各随机选取一名同学,共有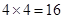 种可能的结果.
种可能的结果.
由茎叶图可知,这两名同学成绩之差的绝对值为3记该事件为A,则该事件A有4种可能的结果,…………10分
因此P(A)=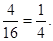 ……………………………………………………12分
……………………………………………………12分
(2)先求出平均分
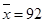 ,然后再利用方差公式计算
,然后再利用方差公式计算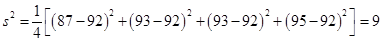 .
.(3)本小题属于古典概型概率问题,先求出从甲、乙两组同学中各随机选取一名同学,共有
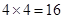 种可能的结果.然后再求出两名同学成绩之差的绝对值为3包含4种可能的结果,
种可能的结果.然后再求出两名同学成绩之差的绝对值为3包含4种可能的结果,所以所求概率
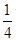 .
.解:(1)依题意,得
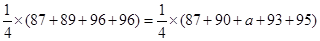 ,……2分
,……2分解得
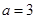 .………………………………………………………………………4分
.………………………………………………………………………4分(2)根据已知条件,可以求得两组同学数学成绩的平均分都为
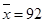 .……………………………5分
.……………………………5分所以乙组四名同学数学成绩的方差为
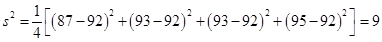 .……………8分
.……………8分(3)分别从甲、乙两组同学中各随机选取一名同学,共有
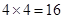 种可能的结果.
种可能的结果.由茎叶图可知,这两名同学成绩之差的绝对值为3记该事件为A,则该事件A有4种可能的结果,…………10分
因此P(A)=
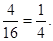 ……………………………………………………12分
……………………………………………………12分
练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
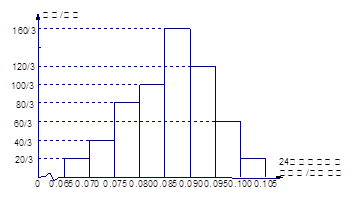

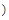 内的人数).图2是统计图1中身高在一定范围内学生人数的一个算法流程图.现要统计身高在[160,180
内的人数).图2是统计图1中身高在一定范围内学生人数的一个算法流程图.现要统计身高在[160,180
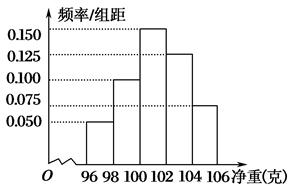
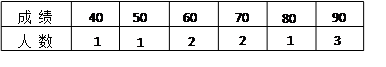
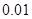 )
)