题目内容
18.设函数f(x)是定义在R上的偶函数,对任意x∈R,都有f(x)=f(x+4),且当x∈[-2,0]时,f(x)=($\frac{1}{2}$)x-1,若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有三个不同的实数根,则a的取值范围是( )| A. | ($\sqrt{3}$,2) | B. | ($\root{3}{4}$,2) | C. | [$\root{3}{4}$,2) | D. | ($\root{3}{4}$,2] |
分析 由已知中f(x)是定义在R上的偶函数,对于任意的x∈R,都有f(x-2)=f(2+x),我们可以得到函数f(x)是一个周期函数,且周期为4,则不难画出函数f(x)在区间(-2,6]上的图象,结合方程的解与函数的零点之间的关系,我们可将方程f(x)-logax+2=0恰有3个不同的实数解,转化为函数f(x)的与函数y=-logax+2的图象恰有3个不同的交点,数形结合即可得到实数a的取值范围.
解答 解:设x∈[0,2],则-x∈[-2,0],
∴f(-x)=($\frac{1}{2}$)-x-1=2x-1,
∵f(x)是定义在R上的偶函数,
∴f(x)=f(-x)=2x-1.
∵对任意x∈R,都有f(x)=f(x+4),
∴当x∈[2,4]时,(x-4)∈[-2,0],
∴f(x)=f(x-4)=xx-4-1;
当x∈[4,6]时,(x-4)∈[0,2],
∴f(x)=f(x-4)=2x-4-1.
∵若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有三个不同的实数根,
∴函数y=f(x)与函数y=loga(x+2)在区间(-2,6]上恰有三个交点,
通过画图可知:恰有三个交点的条件是$\left\{\begin{array}{l}{log}_{a}(6+2)>3\\{log}_{a}(2+2)<3\end{array}\right.$,解得:${2}^{\frac{2}{3}}$<a<2,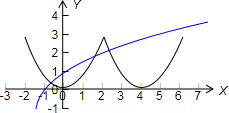
即$\root{3}{4}$<a<2,因此所求的a的取值范围为($\root{3}{4}$,2).
故选:B
点评 本题考查的知识点是根的存在性及根的个数判断,指数函数与对数函数的图象与性质,其中根据方程的解与函数的零点之间的关系,将方程根的问题转化为函数零点问题,是解答本题的关键,体现了转化和数形结合的数学思想,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
| A. | $\frac{5}{4}$ | B. | $\frac{5}{2}$ | C. | 5 | D. | 15 |
| A. | {1,2,3} | B. | {1,$\sqrt{2}$,$\sqrt{3}$,2} | C. | {1,2} | D. | {1} |
 的展开式的常数项为____________.
的展开式的常数项为____________.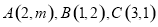 若
若 ,则实数
,则实数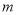 等于( )
等于( )
