题目内容
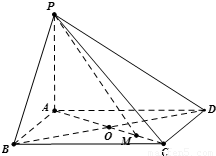 已知四棱锥中,PA⊥平面ABCD,底面ABCD是边长为a的菱形,∠BAD=120°,PA=b.
已知四棱锥中,PA⊥平面ABCD,底面ABCD是边长为a的菱形,∠BAD=120°,PA=b.(I)求证:平面PBD⊥平面PAC;
(II)设AC与BD交于点O,M为OC中点,若二面角O-PM-D的正切值为
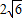 ,求a:b的值.
,求a:b的值.
【答案】分析:(I)根据线面垂直的判定,证明BD⊥平面PAC,利用面面垂直的判定,证明平面PBD⊥平面PAC.
(II)过O作OH⊥PM交PM于H,连HD,则∠OHD为A-PM-D的平面角,利用二面角O-PM-D的正切值为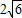 ,即可求a:b的值.
,即可求a:b的值.
解答:(I)证明:因为PA⊥平面ABCD,所以PA⊥BD
又ABCD为菱形,所以AC⊥BD,
因为PA∩AC=A,所以BD⊥平面PAC
因为BD?平面PBD,所以平面PBD⊥平面PAC.
(II)解:过O作OH⊥PM交PM于H,连HD
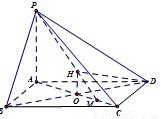
因为DO⊥平面PAC,由三垂线定理可得DH⊥PM,所以∠OHD为A-PM-D的平面角
又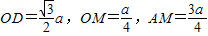 ,且
,且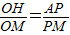
从而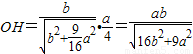
∴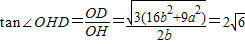
所以9a2=16b2,即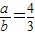 .
.
点评:本题考查线面垂直、面面垂直的判定,考查面面角,解题的关键是掌握线面垂直、面面垂直的判定,作出面面角.
(II)过O作OH⊥PM交PM于H,连HD,则∠OHD为A-PM-D的平面角,利用二面角O-PM-D的正切值为
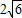 ,即可求a:b的值.
,即可求a:b的值.解答:(I)证明:因为PA⊥平面ABCD,所以PA⊥BD
又ABCD为菱形,所以AC⊥BD,
因为PA∩AC=A,所以BD⊥平面PAC
因为BD?平面PBD,所以平面PBD⊥平面PAC.
(II)解:过O作OH⊥PM交PM于H,连HD

因为DO⊥平面PAC,由三垂线定理可得DH⊥PM,所以∠OHD为A-PM-D的平面角
又
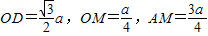 ,且
,且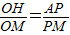
从而
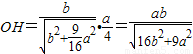
∴
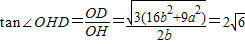
所以9a2=16b2,即
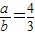 .
.点评:本题考查线面垂直、面面垂直的判定,考查面面角,解题的关键是掌握线面垂直、面面垂直的判定,作出面面角.

练习册系列答案
相关题目
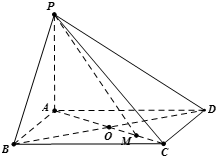 已知四棱锥中,PA⊥平面ABCD,底面ABCD是边长为a的菱形,∠BAD=120°,PA=b.
已知四棱锥中,PA⊥平面ABCD,底面ABCD是边长为a的菱形,∠BAD=120°,PA=b.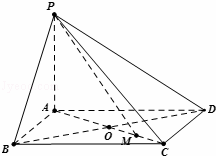
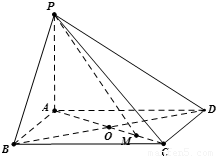 已知四棱锥中,PA⊥平面ABCD,底面ABCD是边长为a的菱形,∠BAD=120°,PA=b.
已知四棱锥中,PA⊥平面ABCD,底面ABCD是边长为a的菱形,∠BAD=120°,PA=b.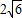 ,求a:b的值.
,求a:b的值.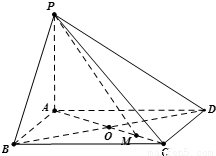 已知四棱锥中,PA⊥平面ABCD,底面ABCD是边长为a的菱形,∠BAD=120°,PA=b.
已知四棱锥中,PA⊥平面ABCD,底面ABCD是边长为a的菱形,∠BAD=120°,PA=b.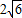 ,求a:b的值.
,求a:b的值.