题目内容
已知2≤x≤8,求函数f(x)=(log2x-1)(log2x-2)的最大值与最小值.
分析:利用换元法将函数转化为二次函数,利用二次函数的性质即可求函数的最值.
解答:解:设t=log2x,
∵2≤x≤8,∴1≤t≤3,
则函数f(x)=(log2x-1)(log2x-2)等价为y=g(t)=(t-1)(t-2)=t2-3t+2=(t-
)2-
,
∵1≤t≤3,
∴当t=
时,g(t)取得最小值-
,
当t=3时,g(t)取得最大值2,
故函数f(x)的最大值与最小值分别为2和-
.
∵2≤x≤8,∴1≤t≤3,
则函数f(x)=(log2x-1)(log2x-2)等价为y=g(t)=(t-1)(t-2)=t2-3t+2=(t-
| 3 |
| 2 |
| 1 |
| 4 |
∵1≤t≤3,
∴当t=
| 3 |
| 2 |
| 1 |
| 4 |
当t=3时,g(t)取得最大值2,
故函数f(x)的最大值与最小值分别为2和-
| 1 |
| 4 |
点评:本题主要考查函数的最值的求法,利用换元法将函数转化为二次函数的解决本题的关键,考查学生的计算能力.

练习册系列答案
相关题目
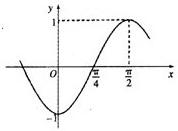 已知函f(x)=sin(ωx+φ)(ω>0,|φ|<π)的部分图象如图所示:
已知函f(x)=sin(ωx+φ)(ω>0,|φ|<π)的部分图象如图所示: