题目内容
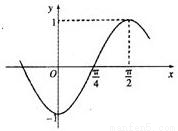
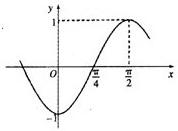 已知函f(x)=sin(ωx+φ)(ω>0,|φ|<π)的部分图象如图所示:
已知函f(x)=sin(ωx+φ)(ω>0,|φ|<π)的部分图象如图所示:(1)求ω,φ的值;
(2)设g(x)=2
| 2 |
| x |
| 2 |
| x |
| 2 |
| π |
| 8 |
| π |
| 2 |
分析:(1)通过函数的图象求出函数周期,求出ω,利用f(0)=-1求出φ,得到函数的解析式.
(2)利用(1)的结果求出g(x)的表达式,当x∈[0,
]时,求出2x+
∈[
,
],然后求出函数的值域.
(2)利用(1)的结果求出g(x)的表达式,当x∈[0,
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
解答:解:(1)由图象知:T=4(
-
)=π,则:ω=
=2,…(2分)
由f(0)=-1得:sinφ=-1,即:φ=kπ-
k∈Z,…(4分)
∵|ω|<π∴φ=-
. …(6分)
(2)由(1)知:f(x)=sin(2x-
)=-cos2x,…(7分)
∴g(x)=2
f(x)f(
-
)-1=2
cosx[
(cosx+sinx)]-1
=cos2x+sin2x=
sin(2x+
),…(10分)
当x∈[0,
]时,2x+
∈[
,
],则sin(2x+
)∈[-
,1],
∴g(x)的值域为[-1,
].…(12分)
| π |
| 2 |
| π |
| 4 |
| 2π |
| T |
由f(0)=-1得:sinφ=-1,即:φ=kπ-
| π |
| 2 |
∵|ω|<π∴φ=-
| π |
| 2 |
(2)由(1)知:f(x)=sin(2x-
| π |
| 2 |
∴g(x)=2
| 2 |
| x |
| 2 |
| π |
| 8 |
| 2 |
| ||
| 2 |
=cos2x+sin2x=
| 2 |
| π |
| 4 |
当x∈[0,
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
| π |
| 4 |
| ||
| 2 |
∴g(x)的值域为[-1,
| 2 |
点评:本题是基础题,考查三角函数的图象的求法,三角函数的化简求值,考查计算能力,常考题型.

练习册系列答案
相关题目
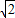 f(
f(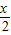 )f(
)f(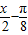 )-1,当x∈[0,
)-1,当x∈[0,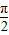 ]时,求函数g(x)的值域.
]时,求函数g(x)的值域.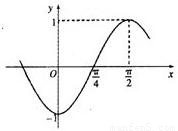
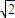 f(
f(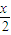 )f(
)f(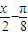 )-1,当x∈[0,
)-1,当x∈[0,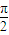 ]时,求函数g(x)的值域.
]时,求函数g(x)的值域.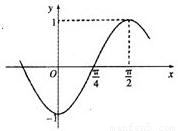
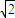 f(
f(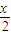 )f(
)f(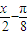 )-1,当x∈[0,
)-1,当x∈[0,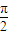 ]时,求函数g(x)的值域.
]时,求函数g(x)的值域.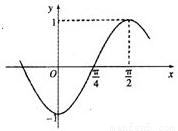
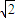 f(
f(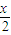 )f(
)f(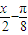 )-1,当x∈[0,
)-1,当x∈[0,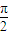 ]时,求函数g(x)的值域.
]时,求函数g(x)的值域.