题目内容
如图，有一直角墙角，两边的长度足够长，在P处有一棵树与两墙的距离分别是
a m(0＜a＜12)、4 m，不考虑树的粗细．现在想用16 m长的篱笆，借助墙角围成一个矩形的
花圃ABCD，设此矩形花圃的面积为S m2，S的最大值为f(a)，若将这棵树围在花圃内，则函数
u＝f(a)的图象大致是( )
C
解析
练习册系列答案
相关题目
设函数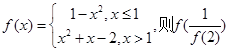
的值为（ ）
A． | B． | C． | D． |
若函数y=x2+(2a－1)x+1在区间（－∞，2
上是减函数，则实数a的取值范围是（ ）
A． － ，+∞） | B．（－∞，－ |
| C．，+∞） | D．（－∞， |
当x∈(0,+∞)时,幂函数y=(m2－m－1)
为减函数, 则实数m的值为( )
| A．m=2 | B．m=－1 | C．m=－1或m=2 | D．m≠ |
已知函数
则实数k的取值范围是（）
| A．(2,3) | B．(-4,0) | C．(-1,-2) | D．[2,3) |
，则函数y＝f(x)的大致图像为： 
设f(x)= 
则f[f(2)]的值为 ( )
| A．0 | B．1 | C．2 | D．3 |
若
，则下列判断正确的是（ ）
A． |
B． |
C． |
D． |
已知函数
，对任意的两个不相等的实数
，都有
成立，且
，则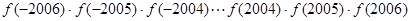 
的值是（ ）
A． | B．1 | C．2006！ | D．（2006！）2 |