题目内容
若函数y=x2+(2a-1)x+1在区间(-∞,2 上是减函数,则实数a的取值范围是( )
上是减函数,则实数a的取值范围是( )
A. - - ,+∞) ,+∞) | B.(-∞,-  |
C.  ,+∞) ,+∞) | D.(-∞,  |
B
解析

练习册系列答案
相关题目
函数 的图象可由函数
的图象可由函数 的图象( )单位得到
的图象( )单位得到
| A.向左平移1个 | B.向右平移1个 | C.向上平移1个 | D.向下平移1个 |
己知关于 的方程
的方程 的两根异号,且负根的绝对值比正根大,那么实数
的两根异号,且负根的绝对值比正根大,那么实数 的取值范围是( )
的取值范围是( )
A.-3<  <0 <0 | B.0< <3 <3 |
C. <- 3或 <- 3或 > 0 > 0 | D. <0 或 <0 或  >3 >3 |
已知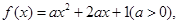 若
若 ,则
,则 与
与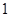 的由大到小的关系式为( )
的由大到小的关系式为( )
A. | B. |
C. | D. |
已知函数 若有
若有 则
则 的取值范围为( )
的取值范围为( )
A. | B. |
C. | D. |
若 ,且
,且 ,则( )
,则( )
A. | B. |
C. | D. |
已知实数 满足等式
满足等式 ,下列五个关系式:①
,下列五个关系式:① ②
② ③
③ ④
④ ⑤
⑤ 其中可能成立的关系式有( )
其中可能成立的关系式有( )
| A.①②③ | B.①②⑤ | C.①③⑤ | D.③④⑤ |
已知 ,则
,则 的值为( )
的值为( )
| A.6 | B.5 | C.4 | D.2 |

