题目内容
6.已知函数$f(x)=1+\frac{a}{{{2^x}+1}}({a∈R})$.(1)当a=-2时,求f(x)的反函数;
(2)当a≥9时,证明函数g(x)=f(x)+2x在[0,1]上是减函数.
分析 (1)a=-2时,得到$f(x)=1-\frac{2}{{2}^{x}+1}$,可设y=f(x),从而可以得到${2}^{x}=\frac{1+y}{1-y}$,进一步得到$x=lo{g}_{2}\frac{1+y}{1-y}$,并可以得到y∈(-1,1),x换y,y换x从而便可得出f(x)的反函数;
(2)先得出$g(x)=\frac{a}{{2}^{x}+1}+{2}^{x}+1$,根据减函数的定义,设任意的x1,x2∈[0,1],且x1<x2,然后作差,通分,提取公因式便可得到$g({x}_{1})-g({x}_{2})=({2}^{{x}_{1}}-{2}^{{x}_{2}})[1-\frac{a}{({2}^{{x}_{1}}+1)({2}^{{x}_{2}}+1)}]$,从而证明g(x1)>g(x2)便可得出g(x)在[0,1]上为减函数.
解答 解:(1)a=-2时,$f(x)=1-\frac{2}{{2}^{x}+1}$,设y=f(x),则:
${2}^{x}=\frac{1+y}{1-y}$;
∴$x=lo{g}_{2}\frac{1+y}{1-y}$;
又${2}^{x}=\frac{1+y}{1-y}$>0;
解得-1<y<1;
∴${f^{-1}}(x)={log_2}\frac{1+x}{1-x}({x∈({-1,1})})$;
(2)证明:$g(x)=\frac{a}{{2}^{x}+1}+{2}^{x}+1$;
设x1,x2∈[0,1],且x1<x2,则:
$g({x}_{1})-g({x}_{2})=\frac{a}{{2}^{{x}_{1}}+1}+{2}^{{x}_{1}}-\frac{a}{{2}^{{x}_{2}}+1}-{2}^{{x}_{2}}$=$({2}^{{x}_{1}}-{2}^{{x}_{2}})[1-\frac{a}{({2}^{{x}_{1}}+1)({2}^{{x}_{2}}+1)}]$;
∵0≤x1<x2≤1,∴${2^{x_1}}-{2^{x_2}}<0$,4<$({2^{x_1}}+1)({2^{x_2}}+1)<9$;
又a≥9;
∴$1-\frac{a}{({2}^{{x}_{1}}+1)({2}^{{x}_{2}}+1)}<0$;
∴g(x1)>g(x2);
∴当a≥9时,函数g(x)=f(x)+2x在[0,1]上是减函数.
点评 考查反函数的概念及其求法,分式不等式的解法,指数函数的值域,指数函数的单调性,不等式的性质,以及减函数的定义,根据减函数的定义证明一个函数为减函数的方法和过程,作差的方法比较g(x1),g(x2)的大小,作差后是分式的一般要通分,一般要提取公因式.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案| A. | π+2 | B. | $\frac{π}{2}$+2 | C. | $\frac{3π}{2}$-2 | D. | 2-$\frac{π}{2}$ |
| x | 2 | 3 | 4 | 5 | 6 |
| y | 11 | 15 | 19 | 26 | 29 |
参考公式:b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\overline{a}$=$\overline{y}$-b$\overline{x}$.
(1)求每一个技术员被抽到的概率及该新产品研发小组中男、女技术员的人数;
(2)一年后研发小组决定选两名研发的技术员对该项研发产品进行检验,方法是先从研发小组中选一人进行检验,该技术员检验结束后,再从研发小组内剩下的三名技术员中选一人进行检验,若两名技术员检验得到的数据如下:
| 第一次被抽到进行检验的技术员 | 58 | 53 | 87 | 62 | 78 | 70 | 82 |
| 第二次被抽到进行检验的技术员 | 64 | 61 | 78 | 66 | 74 | 71 | 76 |
请问哪位技术员检验更稳定?并说明理由.
| A. | 6 | B. | 12 | C. | 24 | D. | 36 |
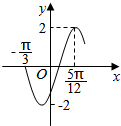 函数f(x)=2sin(ωx+φ)$(ω>0,-\frac{π}{2}<φ<\frac{π}{2})$的部分图象如图所示,则f(x)的单调增区间是[kπ-$\frac{π}{12}$,$\frac{5π}{12}+kπ$].
函数f(x)=2sin(ωx+φ)$(ω>0,-\frac{π}{2}<φ<\frac{π}{2})$的部分图象如图所示,则f(x)的单调增区间是[kπ-$\frac{π}{12}$,$\frac{5π}{12}+kπ$].