题目内容
在△ABC中,若sin(2π-A)=-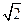 sin(π-B),
sin(π-B),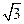 cosA=-
cosA=-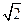 cos(π-B),
cos(π-B),
求△ABC的三内角.

(1)当cosA=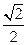 时,cosB=
时,cosB= ,又A、B是三角形内角,
,又A、B是三角形内角,
∴A= ,B=
,B= ,∴C=π-(A+B)=
,∴C=π-(A+B)= π.
π.
(2)当cosA=-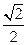 时,cosB=-
时,cosB=- .又A、B是三角形内角,
.又A、B是三角形内角,
∴A= π,B=
π,B=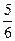 π,不合题意.
π,不合题意.
综上知,A= ,B=
,B= ,C=
,C= π.
π.
解析

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
函数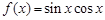 的最小值是( )
的最小值是( )
| A.1 | B.-1 | C.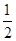 | D.-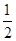 |
 的图象经过点
的图象经过点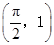 .
.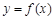 的解析式,并求函数的最小正周期和最大值.
的解析式,并求函数的最小正周期和最大值.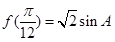 ,其中
,其中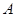 是面积为
是面积为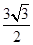 的锐角
的锐角 的内角,且
的内角,且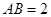 ,
, 和
和 的长.
的长.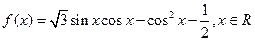 .
.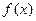 的最小值和最小正周期;
的最小值和最小正周期; 内角
内角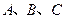 的对边分别为
的对边分别为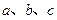 ,且
,且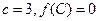 ,若向量
,若向量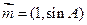 与
与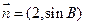 共线,求
共线,求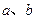 的值.
的值.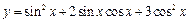 .
.
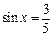 ,且
,且 为第一象限角,求y的值;
为第一象限角,求y的值;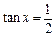 ,求y的值.
,求y的值.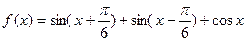
 的最小正周期;
的最小正周期;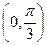 的值域。
的值域。 是方程
是方程 的两根
的两根 的值 (II)求
的值 (II)求 的值
的值 向量
向量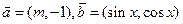 ,
,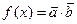 且满足
且满足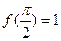 .
.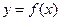 的解析式;
的解析式;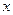 值;
值;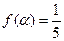 ,求
,求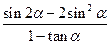 的值.
的值. ,
, 1)求
1)求 的值;
的值;