题目内容
若“对?x∈[1，2]，都有x2+ax+1≥0时a的取值范围”是“实数a＞3”的 ________条件（填写“充分不必要”、“必要不充分”、“充要”或“既不充分也不必要”）
必要不充分
分析：首先要找?x∈[1，2]，都有x2+ax+1≥0恒成立a的范围，可以转化为求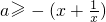
在[1，2]上的最大值，根据命题之间的关系求解．
解答：∵对?x∈[1，2]，都有x2+ax+1≥0
∴ax≥-（x2+1） 即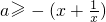
而函数
在[1，2]上单调递增
∴
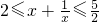
∴a≥-2
由a≥-2不能推出a＞3，而由a＞3可推出a≥-2
故答案为：必要不充分条件
点评：本题考查充要条件的知识，解题的关键是将恒成立问题转化为最值问题处理，属于基础题．
分析：首先要找?x∈[1，2]，都有x2+ax+1≥0恒成立a的范围，可以转化为求
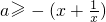在[1，2]上的最大值，根据命题之间的关系求解．解答：∵对?x∈[1，2]，都有x2+ax+1≥0
∴ax≥-（x2+1） 即
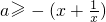
而函数
在[1，2]上单调递增∴
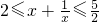
∴a≥-2
由a≥-2不能推出a＞3，而由a＞3可推出a≥-2
故答案为：必要不充分条件
点评：本题考查充要条件的知识，解题的关键是将恒成立问题转化为最值问题处理，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目