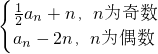题目内容
己知数列{An}中,A1>-1,对任意自然数n,都有An+1=![]() .
.
(1) 设A1=1,求A2,A3,A4;
(2)
试比较An与![]() 的大小,并证明你的结论;
的大小,并证明你的结论;
(3)
当A1≠![]() 时,证明:对于任意自然数n,或者都满足A2n-1<A2n+1;或者都满足A2n-1<A2n+1。
时,证明:对于任意自然数n,或者都满足A2n-1<A2n+1;或者都满足A2n-1<A2n+1。
答案:
解析:
解析:
(1)依A1=1,可以依次推得: A2= (2)依A1>-1及An+1= 可以推得An>-1. 研究An+1- = 注意到: ①当A1= 因此对于任意自然数n,An= ②当-1<A1< 因此,当n是奇数时An< ③当A1> 当n是奇数时,An> (3)研究A2n+1-A2n-1=(1+ =1+ = ①
当-1<A1< ②
当A1> 因此,对任意自然数n,有A2n+1<A2n-1. |

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
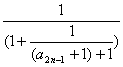
 .
.