题目内容
己知数列{an}满足:a1=1,an+1=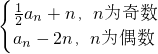
(1)求a2,a3;
(2)设bn=a2n-2,n∈N*,求证{bn} 是等比数列,并求其通项公式;
(3)在(2)条件下,求数列{an} 前100项中的所有偶数项的和S.
解:(Ⅰ)由题意可得, =
= ,a3=a2-4=
,a3=a2-4= ,(4分)
,(4分)
(Ⅱ)∵ =
=
=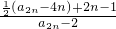 =
= =
= (6分)
(6分)
∵ (9分)
(9分)
∴数列{bn}是等比数列,且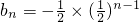 =
=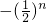 (l0分)
(l0分)
(Ⅲ)由(Ⅱ)得a2n=bn+2= (n=1,2,…50)(12分)
(n=1,2,…50)(12分)
∴S=a2+a4+…+a100=2×50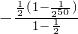
= =99+
=99+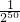 (14分)
(14分)
分析:(1)直接把n=2,3代入数列递推公式即可求出a2,a3;
(2)由题意可得bn+1=a2n+2-2= a2n+1+(2n+1)-2=
a2n+1+(2n+1)-2= a2n-1=
a2n-1= bn,然后根据比数列来求数列{bn}的通项公式;
bn,然后根据比数列来求数列{bn}的通项公式;
(3)把数列{an}中的所有项都用数列{bn}的通项表示出来,再采用分组求和法求其前100项的和即可.
点评:题主要考查数列递推关系式的应用以及数列求和的分组求和法,是对数列知识的综合考查,具有一定的综合性.
 =
= ,a3=a2-4=
,a3=a2-4= ,(4分)
,(4分)(Ⅱ)∵
 =
=
=
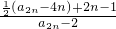 =
= =
= (6分)
(6分)∵
 (9分)
(9分)∴数列{bn}是等比数列,且
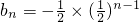 =
=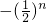 (l0分)
(l0分)(Ⅲ)由(Ⅱ)得a2n=bn+2=
 (n=1,2,…50)(12分)
(n=1,2,…50)(12分)∴S=a2+a4+…+a100=2×50
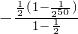
=
 =99+
=99+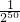 (14分)
(14分)分析:(1)直接把n=2,3代入数列递推公式即可求出a2,a3;
(2)由题意可得bn+1=a2n+2-2=
 a2n+1+(2n+1)-2=
a2n+1+(2n+1)-2= a2n-1=
a2n-1= bn,然后根据比数列来求数列{bn}的通项公式;
bn,然后根据比数列来求数列{bn}的通项公式;(3)把数列{an}中的所有项都用数列{bn}的通项表示出来,再采用分组求和法求其前100项的和即可.
点评:题主要考查数列递推关系式的应用以及数列求和的分组求和法,是对数列知识的综合考查,具有一定的综合性.

练习册系列答案
相关题目