题目内容
设函数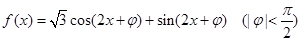 ,且其图象关于直线
,且其图象关于直线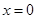 对称,则 ( )
对称,则 ( )
A.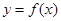 的最小正周期为 的最小正周期为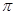 ,且在 ,且在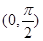 上为增函数 上为增函数 |
B.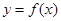 的最小正周期为 的最小正周期为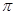 ,且在 ,且在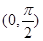 上为减函数 上为减函数 |
C.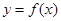 的最小正周期为 的最小正周期为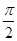 ,且在 ,且在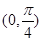 上为增函数 上为增函数 |
D.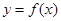 的最小正周期为 的最小正周期为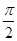 ,且在 ,且在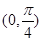 上为减函数 上为减函数 |
B
解析试题分析:根据题意,由于函数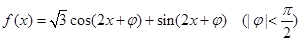 ,则可知其解析式化简为
,则可知其解析式化简为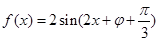 ,那么结合三角函数性质,由于图象关于直线
,那么结合三角函数性质,由于图象关于直线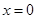 对称,说明是偶函数,可知
对称,说明是偶函数,可知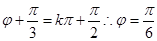 ,可知周期为
,可知周期为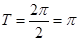 ,故排除C,D,然后对于函数给定的区间上,因为
,故排除C,D,然后对于函数给定的区间上,因为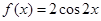 ,可知在原点附近的区间
,可知在原点附近的区间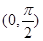
单调递减,故选B.
考点:三角函数的性质
点评:解决该试题的关键是对于函数解析式的化简,然后结合三角函数的性质来分析,属于基础题。

练习册系列答案
相关题目
若将函数
 的图象向右平移
的图象向右平移 个单位长度后与函数
个单位长度后与函数 的图象重合,则
的图象重合,则 的最小值为( )
的最小值为( )
| A.1 | B.2 | C. | D. |
下列函数中,在区间(0,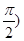 上为增函数且以
上为增函数且以 为周期的函数是
为周期的函数是
A.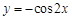 | B. | C. | D. |
要得到函数y=cos(2x+1)的图象,只需将函数y=cos2x的图象
| A.向左平移1个单位 | B.向右平移1个单位 |
C.向左平移 个单位 个单位 | D.向右平移 个单位 个单位 |
已知函数 的最小正周期为
的最小正周期为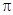 ,下列四个判断:
,下列四个判断:
(1)当 时,
时, 的最小值为
的最小值为 ;
;
(2)函数 的图象关于直线
的图象关于直线 对称;
对称;
(3)函数 的图象可由
的图象可由 的图象向右平移
的图象向右平移 个单位长度得到;
个单位长度得到;
(4)函数 在区间
在区间 上是减函数.
上是减函数.
则正确判断的个数是
| A.1 | B.2 | C.3 | D.4 |
已知奇函数f(x)在[-1,0]上为单调递减函数,又a,b为锐角三角形两内角,下列结论正确的是
| A.f(cosa)> f(cosb) | B.f(sina)> f(sinb) |
| C.f(sina)> f(cosb) | D.f(sina)<f(cosb) |
已知函数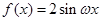 在区间
在区间 上的最小值是
上的最小值是 ,则
,则 的取值范围为( )
的取值范围为( )
A. | B. |
C. | D. |
已知 为第二象限角,则
为第二象限角,则 的值是( )
的值是( )
| A.3 | B.-3 | C.1 | D.-1 |
 的图象向左平移
的图象向左平移 个单位,再把所得函数图象上所有点的横坐标伸长为原来的2倍(纵坐标不变),得到图象的解析式为( )
个单位,再把所得函数图象上所有点的横坐标伸长为原来的2倍(纵坐标不变),得到图象的解析式为( )


