题目内容
某医药研究所开发一种新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.

(1)写出服药后y与t之间的函数关系式y=f(t);
(2)据进一步测定:每毫升血液中含药量不少于0.25微克时,治疗疾病有效.
①求服药一次治疗疾病有效的时间?
②当t=5时,第二次服药,问t![]() 时,药效是否连续?
时,药效是否连续?
答案:
解析:
解析:
|
解答:(1)当0≤t≤1时,y=4 t, 当t≥1时, (2)① ∴服药一次治疗疾病有效的时间为 ②设 只要证明,当 ∴当t=5时,第二次服药, |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
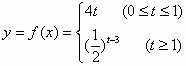
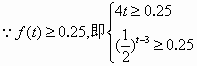 解得
解得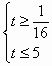
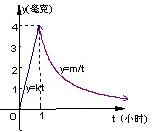 某医药研究所开发一种新药,成年人按规定的剂量限用,服药后每毫升血液中的含药量y(毫克)与时间t(小时)之间的函数关系近似满足如图所示曲线,当每毫升血液中的含药量不少于0.25毫克时治疗有效,则服药一次治疗疾病有效的时间为
某医药研究所开发一种新药,成年人按规定的剂量限用,服药后每毫升血液中的含药量y(毫克)与时间t(小时)之间的函数关系近似满足如图所示曲线,当每毫升血液中的含药量不少于0.25毫克时治疗有效,则服药一次治疗疾病有效的时间为
 某医药研究所开发一种新药,据监测,如果成人按规定的剂量服用该药,服药后每毫升血液中的含药量y(μg)与服药后的时间t(h)之间近似满足如图所示的曲线.其中OA是线段,曲线段AB是函数y=k•at(t≥1,a>0,k,a是常数)的图象.
某医药研究所开发一种新药,据监测,如果成人按规定的剂量服用该药,服药后每毫升血液中的含药量y(μg)与服药后的时间t(h)之间近似满足如图所示的曲线.其中OA是线段,曲线段AB是函数y=k•at(t≥1,a>0,k,a是常数)的图象. 我市沿海某医药研究所开发一种新药,如果成年人按规定的剂量服用,据监测,服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线(OA为线段,AB为某二次函数图象的一部分,B是抛物线顶点,O为原点).
我市沿海某医药研究所开发一种新药,如果成年人按规定的剂量服用,据监测,服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线(OA为线段,AB为某二次函数图象的一部分,B是抛物线顶点,O为原点). 某医药研究所开发一种抗甲流新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.
某医药研究所开发一种抗甲流新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.