题目内容
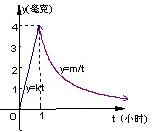 某医药研究所开发一种新药,成年人按规定的剂量限用,服药后每毫升血液中的含药量y(毫克)与时间t(小时)之间的函数关系近似满足如图所示曲线,当每毫升血液中的含药量不少于0.25毫克时治疗有效,则服药一次治疗疾病有效的时间为
某医药研究所开发一种新药,成年人按规定的剂量限用,服药后每毫升血液中的含药量y(毫克)与时间t(小时)之间的函数关系近似满足如图所示曲线,当每毫升血液中的含药量不少于0.25毫克时治疗有效,则服药一次治疗疾病有效的时间为
分析:将点(1,4)分别代入y=kt,y=
中,求k、m,确定函数关系式,再把y=0.25代入两个函数式中求t,把所求两个时间t作差即可.
| m |
| t |
解答:解:把点(1,4)分别代入y=kt,y=
中,得k=4,m=4,
∴y=4t,y=
,
把y=0.25代入y=4t中,得t1=
=
,
把y=0.25代入y=
中,得t2=
=16,
∴治疗疾病有效的时间为:t2-t1=16-0.0625=16-
=15
;
故答案为:15
.
| m |
| t |
∴y=4t,y=
| 4 |
| t |
把y=0.25代入y=4t中,得t1=
| 0.25 |
| 4 |
| 1 |
| 16 |
把y=0.25代入y=
| 4 |
| t |
| 4 |
| 0.25 |
∴治疗疾病有效的时间为:t2-t1=16-0.0625=16-
| 1 |
| 16 |
| 15 |
| 16 |
故答案为:15
| 15 |
| 16 |
点评:本题考查了本题主要考查函数模型的选择与应用、反比例函数、一次函数的实际应用.关键是用待定系数法求函数关系式,理解题意,根据已知函数值求自变量的差.

练习册系列答案
相关题目
 某医药研究所开发一种新药,据监测,如果成人按规定的剂量服用该药,服药后每毫升血液中的含药量y(μg)与服药后的时间t(h)之间近似满足如图所示的曲线.其中OA是线段,曲线段AB是函数y=k•at(t≥1,a>0,k,a是常数)的图象.
某医药研究所开发一种新药,据监测,如果成人按规定的剂量服用该药,服药后每毫升血液中的含药量y(μg)与服药后的时间t(h)之间近似满足如图所示的曲线.其中OA是线段,曲线段AB是函数y=k•at(t≥1,a>0,k,a是常数)的图象. 我市沿海某医药研究所开发一种新药,如果成年人按规定的剂量服用,据监测,服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线(OA为线段,AB为某二次函数图象的一部分,B是抛物线顶点,O为原点).
我市沿海某医药研究所开发一种新药,如果成年人按规定的剂量服用,据监测,服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线(OA为线段,AB为某二次函数图象的一部分,B是抛物线顶点,O为原点). 某医药研究所开发一种抗甲流新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.
某医药研究所开发一种抗甲流新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.