题目内容
(14分)设函数f(x)=xn(n≥2,n∈N*)
(1)若Fn(x)=f(x-a)+f(b-x)(0<a<x<b),求Fn(x)的取值范围;
(2)若Fn(x)=f(x-b)-f(x-a),对任意n≥a (2≥a>b>0),
证明:F (n)≥n(a-b)(n-b)n-2。
(n)≥n(a-b)(n-b)n-2。
(1)[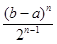 ,(b-a)n)
,(b-a)n)
(2)略
【解析】1)∵Fn(x)=f (x-a)+f(b-x)=(x-a)n+(b-x)n
F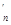 (x)=n(x-a)n-1+n(b-x)n-1·(-1)=n[(x-a)n-1-(b-x)n-1]
(x)=n(x-a)n-1+n(b-x)n-1·(-1)=n[(x-a)n-1-(b-x)n-1]
令F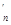 (x)=0得(x-a)n-1=(b-x)n-1
(x)=0得(x-a)n-1=(b-x)n-1
∵0<a<x<b ∴f (x)=xn(n≥2,n∈N+)为单调增函数
∴x=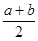
|
x |
(a, |
|
( |
|
F |
- |
0 |
+ |
|
F |
单调减 |
极小值 |
单调增 |
∴Fn(x)min=Fn(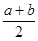 )=(
)=(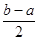 )n+(
)n+(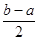 )n=
)n=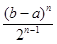
又Fn(x)在x=a,x=b处连续且Fn(a)=Fn(b)=(b-a)n
故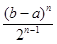 ≤Fn(x)<(b-a)n
≤Fn(x)<(b-a)n
即Fn(x)的取值范围为[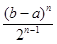 ,(b-a)n)………………………………7分
,(b-a)n)………………………………7分
(2)证明:∵Fn(x)=f(x-b)-f(x-a)=(x-b)n-(x-a)n
∴F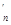 (x)=n[(x-b)n-1-(x-a)n-1]
(x)=n[(x-b)n-1-(x-a)n-1]
则F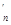 (n)=n[(n-b)n-1-(n-a)n-1]
(n)=n[(n-b)n-1-(n-a)n-1]
∵当x≥a>0时F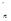 (x)>0
(x)>0
∴当x≥a>0时Fn(x)是关于x的增函数
∴当n≥a时,(n+1-b)n-(n+1-a)n>(n-b)n-(n-a)n>0
∴F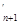 (n+1)=(n+1)[(n+1-b)n-(n+1-a)n]>(n+1)[(n-b)n-(n-a)n]
(n+1)=(n+1)[(n+1-b)n-(n+1-a)n]>(n+1)[(n-b)n-(n-a)n]
>(n+1)[(n-b) (n-b)n-1-(n-b) (n-a)n-1]
=(n+1)(n-b)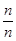 [(n-b)n-1-(n-a)n-1]
[(n-b)n-1-(n-a)n-1]
=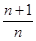 (n-b)·F
(n-b)·F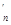 (n)
(n)
而F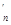 (n)>0
(n)>0
于是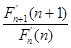 >
>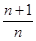 ·(n-b)
·(n-b)
而F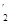 (2)=2[(2-b)2-1-(2-a)2-1]=2(a-b)
(2)=2[(2-b)2-1-(2-a)2-1]=2(a-b)
当n≥3时
F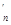 (n)=
(n)=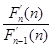 ·
·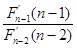 …
…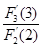 ·F
·F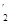 (2)
(2)
>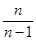 ·
·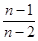 …
…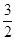 ·2(a-b) ·(n-b)n-2
·2(a-b) ·(n-b)n-2
=n(a-b)(n-b)n-2
即F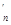 (n) ≥n(a-b)(n-b)n-2…………………………………………………14分
(n) ≥n(a-b)(n-b)n-2…………………………………………………14分

 一线名师提优试卷系列答案
一线名师提优试卷系列答案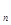 (x)
(x) (n)≥n(a-b)(n-b)n-2。
(n)≥n(a-b)(n-b)n-2。