题目内容
20.在等比数列{an}中,a1=1,a3,a2+a4,a5成等差数列.(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1+$\frac{{b}_{2}}{2}$+…+$\frac{{b}_{n}}{n}$=an(n∈N•),{bn}的前n项和为Sn,求满足Sn-1>an+bn的n的最小值.
分析 (1)通过a3,a2+a4,a5成等差数列,可得q=2,进而可得结论;
(2)通过b1+$\frac{{b}_{2}}{2}$+…+$\frac{{b}_{n}}{n}$=an(n∈N*),可得bn=$\left\{\begin{array}{l}{1,}&{n=1}\\{n•{2}^{n-2},}&{n≥2}\end{array}\right.$,易得当n=1时不满足题意;当n≥2时利用错位相减法计算即可.
解答 解:(1)设数列{an}的公比为q,
∵a3,a2+a4,a5成等差数列,
∴2(a2+a4)=a3+a5,
即2(q+q3)=q2+q4,解q=2,
又∵a1=1,∴an=2n-1;
(2)∵b1+$\frac{{b}_{2}}{2}$+…+$\frac{{b}_{n}}{n}$=an(n∈N*),
∴当n=1时,b1=a1=1,
当n≥2时,$\frac{{b}_{n}}{n}$=an-an-1=2n-2,
∴bn=n•2n-2,即bn=$\left\{\begin{array}{l}{1,}&{n=1}\\{n•{2}^{n-2},}&{n≥2}\end{array}\right.$,
∴当n=1时,S1=b1=1,∴S1-1=0,不满足S1-1>a1+b1;
当n≥2时Sn=1+2×20+3×21+…+n×2n-2,
∴2Sn=2+2×21+3×22+…+n×2n-1,
两式相减得:-Sn=1+21+…+2n-2-n×2n-1
=$\frac{1-{2}^{n-1}}{1-2}-n×{2}^{n-1}$=(1-n)2n-1-1,
∴Sn=1+(n-1)2n-1.
要使Sn-1>an+bn,只需(n-1)2n-1>2n-1+n×2n-2,
解得n>4,
∴满足Sn-1>an+bn的n的最小值为5.
点评 本题考查等差数列、等比数列的概念及性质,考查分类讨论的思想,注意解题方法的积累,属于中档题.

| 队别 | 北京 | 黑龙江 | 辽宁 | 八一 |
| 人数 | 4 | 6 | 3 | 5 |
(Ⅱ)若要求选出两位队员当正副队长,设其中来自北京队的人数为ξ,求随机变量ξ的分布列及数学期望Eξ.
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
| A. | $\frac{2}{3}π$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{12}$ |

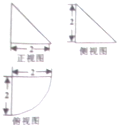 某几何体的三视图如图所示,其中正视图和侧视图均为等腰直角三角形,俯视图是圆心角为直角的扇形,则该几何体的体积为$\frac{2π}{3}$.
某几何体的三视图如图所示,其中正视图和侧视图均为等腰直角三角形,俯视图是圆心角为直角的扇形,则该几何体的体积为$\frac{2π}{3}$.