题目内容
已知函数f(x)=2+(1)求a的值,使得a3=0;
(2)设数列{bn}满足b1=-![]() ,bn=f(bn+1)(n∈N*),求证:不论a取{bn}中的何数,都可以得到一个有穷数列{an};
,bn=f(bn+1)(n∈N*),求证:不论a取{bn}中的何数,都可以得到一个有穷数列{an};
(3)求a的取值范围,使得当n≥2时,都有![]() <an<3.
<an<3.
(1)解:因为a1=a,an+1=2+![]() ,所以a2=2+
,所以a2=2+![]() ,a3=2+
,a3=2+![]() .
.
要a3=0,即要a=-![]() .所以,a=-
.所以,a=-![]() 时,a3=0.
时,a3=0.
(2)证明:由题知b1=-![]() ,2+
,2+![]() =bn.
=bn.
不妨设a取bn,所以a2=2+![]() =bn-1,a3=2+
=bn-1,a3=2+![]() =2+
=2+![]() =bn-2,
=bn-2,
……
an=2+![]() =2+
=2+![]() =b1=-
=b1=-![]() .
.
所以a n+1=0.
所以不论a取{bn}中的何数,都可以得到一个有穷数列{an}.
(3)解:![]() <an<3
<an<3![]()
![]() <2+
<2+![]() <3
<3![]() 1<an-1<3.
1<an-1<3.
因为(![]() ,3)
,3)![]() (1,3),所以只要有
(1,3),所以只要有![]() <a2<3就有
<a2<3就有![]() <an<3(n≥3).
<an<3(n≥3).
由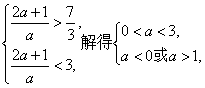 即1<a<3.
即1<a<3.
所以a的取值范围是(1,3).

练习册系列答案
相关题目