题目内容
有共同底边的等边三角形ABC和BCD所在平面互相垂直,则异面直线AB和CD所成角的余弦值为( )
分析:先根据面面垂直的性质定理证明AO⊥BC⊥OD,从而建立空间直角坐标系,再分别写出相关点的坐标以及
,
的坐标,最后由夹角公式计算异面直线AB和CD所成角的余弦值即可
| AB |
| CD |
解答:解:如图: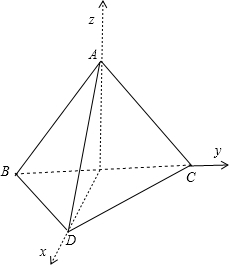 设等边三角形的边长为2.
设等边三角形的边长为2.
∵等边三角形ABC和BCD所在平面互相垂直
∴取BC中点O,则AO⊥BC⊥OD
以O为原点,建立如图空间直角坐标系
则A(0,0,
),B(0,-1,0),C(0,1,0),D(
,0,0)
∴
=(0,-1,-
),
=(
,-1,0)
∴cos<
,
>=
=
=
∴异面直线AB和CD所成角的余弦值
故选C
 设等边三角形的边长为2.
设等边三角形的边长为2.∵等边三角形ABC和BCD所在平面互相垂直
∴取BC中点O,则AO⊥BC⊥OD
以O为原点,建立如图空间直角坐标系
则A(0,0,
| 3 |
| 3 |
∴
| AB |
| 3 |
| CD |
| 3 |
∴cos<
| AB |
| CD |
| ||||
|
|
| 1 |
| 2×2 |
| 1 |
| 4 |
∴异面直线AB和CD所成角的余弦值
| 1 |
| 4 |
故选C
点评:本题考查了利用空间直角坐标系求异面直线所成的角的方法,将空间角问题转化为向量夹角问题的思想方法

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
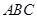 和
和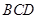 所在平面互相垂直,则异面直线
所在平面互相垂直,则异面直线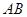 和
和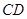 所成角的余弦值为
( )
所成角的余弦值为
( )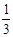 B.
B.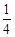 C.
C. D.
D.